5.29 エルミート行列の対角化
定義 5.90 (エルミート行列)
行列
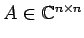 が
が 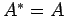 をみたすとき
をみたすとき
 をエルミート行列(Hermite matrix)という.
をエルミート行列(Hermite matrix)という.
注意 5.91 (エルミート行列と対称行列)
エルミート行列  の要素が実数のみであるとき,
の要素が実数のみであるとき,
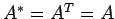 よりエルミート行列は対称行列となる.
よりエルミート行列は対称行列となる.
定理 5.92 (エルミート行列の固有値)
エルミート列の固有値はすべて実数である.
が成り立つ. ここで,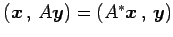 を用いた.
を用いた.
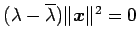 ,
,
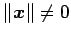 より,
より,
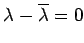 が成立する.
が成立する.
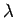 は実数である.
は実数である.
(証明)
![]() とし,
とし,
![]() 上の内積を用いて,
上の内積を用いて,
が成り立つ. ここで,
注意 5.93 (エルミート行列)
エルミート行列は正規行列である.
定理 5.94 (エルミート行列の固有ベクトル)
エルミート行列において,
異なる固有値に属する固有ベクトルは直交する.
となる.
であるから,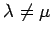 より
より
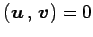 を得る.
を得る.
(証明)
エルミート行列は正規行列であるので固有ベクトルは直交する.
または,次のように示す.
![]() ,
,
![]() ,
,
![]() ,
,
![]() (
(
![]() ) とする.
) とする.
![]() 上の内積を用いて,
上の内積を用いて,
となる.
であるから,
定理 5.95 (エルミート行列の対角化)
エルミート行列
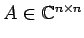 の
固有値を
の
固有値を
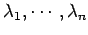 とする.
このとき,
とする.
このとき, は
ユニタリー行列
は
ユニタリー行列
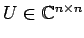 を用いて
を用いて
と対角化される. ただし,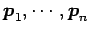 は
は
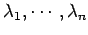 の固有ベクトルであり,
の固有ベクトルであり,
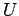 がユニタリー行列となるように選ぶとする.
がユニタリー行列となるように選ぶとする.
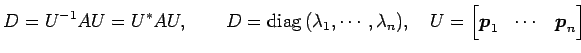 |
と対角化される. ただし,
例 5.96 (エルミート行列の対角化の具体例)
行列
を対角化する.
より,固有値は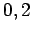 である.
である.
より,固有ベクトルはそれぞれ
となる.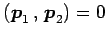 であるから,
規格化して
であるから,
規格化して
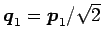 ,
,
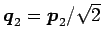 とする.
このとき
とする.
このとき  はユニタリー行列
はユニタリー行列  を用いて
を用いて
と対角化される.
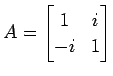 |
を対角化する.
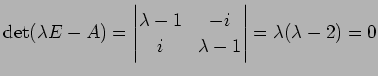 |
より,固有値は
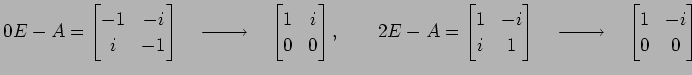 |
より,固有ベクトルはそれぞれ
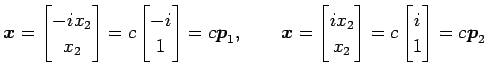 |
となる.
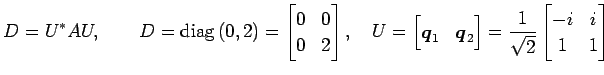 |
と対角化される.
例 5.97 (エルミート行列の対角化の具体例)
行列
を対角化する.
より,固有値は (2 個),
(2 個), 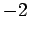 である.
である.
より,固有ベクトルはそれぞれ
となる.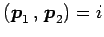 ,
,
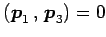 ,
,
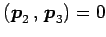 であるから,
であるから,
とおくと, 正規直交系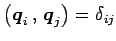 となる.
このとき
となる.
このとき  はユニタリー行列
はユニタリー行列  を用いて
を用いて
と対角化される.
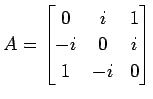 |
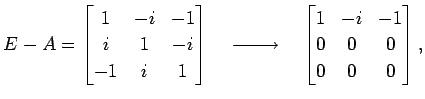
を対角化する.
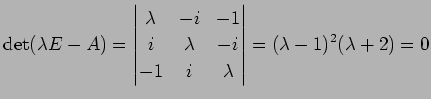 |
より,固有値は
 |
||
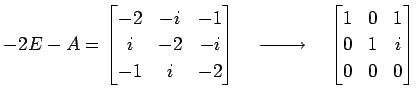 |
より,固有ベクトルはそれぞれ
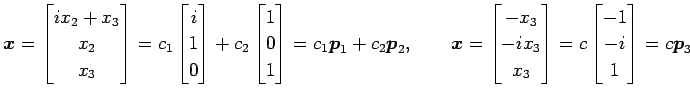 |
となる.
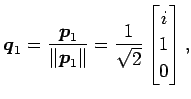 |
||
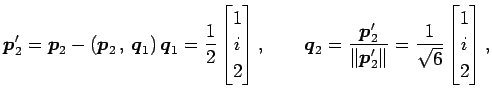 |
||
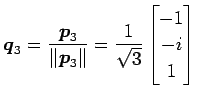 |
とおくと, 正規直交系
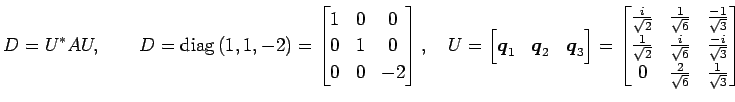 |
と対角化される.
Kondo Koichi

平成18年1月17日