5.24 2 次対称行列の対角化
例 5.71 (対称行列の対角化の具体例)
対称行列
を直交行列で対角化する. の固有多項式は
の固有多項式は
であるから, 固有値は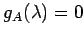 より
より
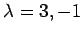 となる.
となる.
より,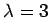 と
と
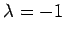 に
属する固有ベクトルはそれぞれ
に
属する固有ベクトルはそれぞれ
となる.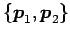 は1 次独立であるから,
は1 次独立であるから,
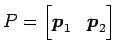 は正則となる.
しかし
は正則となる.
しかし 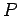 は直交行列ではないので,
直交行列となるように固有ベクトルを選び直す.
は直交行列ではないので,
直交行列となるように固有ベクトルを選び直す.
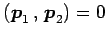 であるから,
であるから,
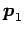 と
と 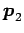 は直交する.
よってこれらを正規化すればよい.
は直交する.
よってこれらを正規化すればよい.
とおくと,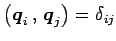 (
(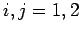 )
が成り立ち正規直交系となる.
以上より行列
)
が成り立ち正規直交系となる.
以上より行列  は
は
と直交行列 で対角化される.
で対角化される.
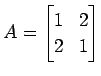 |
を直交行列で対角化する.
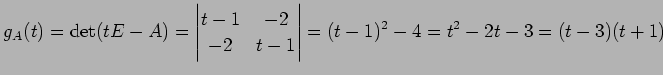 |
であるから, 固有値は
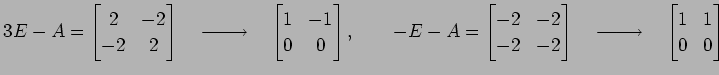 |
より,
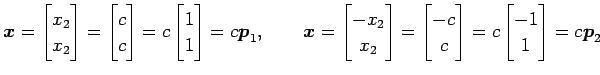 |
となる.
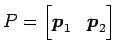 は正則となる.
しかし
は正則となる.
しかし 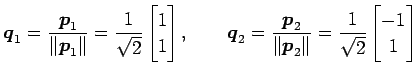 |
とおくと,
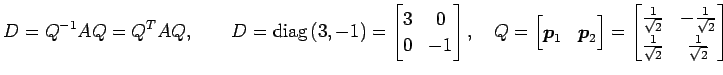 |
と直交行列
注意 5.72 (対称行列の固有空間)
線形変換
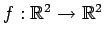 ;
;
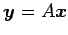 の
固有空間は
の
固有空間は
である.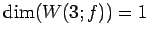 ,
,
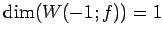 ,
,
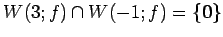 より
より
を得る. 固有空間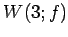 ,
, 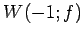 は
は
 の直和分解である.
また,異なる固有値に属する固有ベクトルは直交するので,
固有空間も直交し
の直和分解である.
また,異なる固有値に属する固有ベクトルは直交するので,
固有空間も直交し
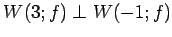 を得る.
を得る.
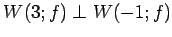 と(☆)より,
と(☆)より,
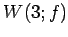 は
は
 における
における 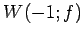 の直交補空間となる.
また逆に
の直交補空間となる.
また逆に
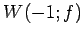 は
は
 における
における 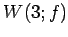 の直交補空間となる.
の直交補空間となる.
である.
を得る. 固有空間
Kondo Koichi

平成18年1月17日