5.23 対称行列の対角化
定義 5.61 (対称行列)
行列
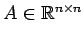 が
が
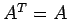 をみたすとき,
をみたすとき, を
対称行列(symmetric matrix)という.
を
対称行列(symmetric matrix)という.
注意 5.62 (対称行列)
対称行列は
の形で表される.
 |
の形で表される.
例 5.63 (対称行列の具体例)
次に行列は対称行列である.
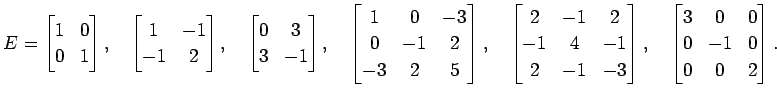 |
定義 5.64 (共役行列)
行列
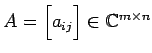 に対して
に対して
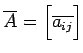 と定義する.
と定義する.
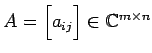 に対して
に対して
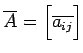 と定義する.
と定義する.
定義 5.65 (共役転置行列)
行列
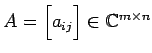 に対して
共役転置行列を
に対して
共役転置行列を
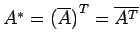 と定義する.
と定義する.
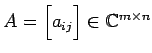 に対して
共役転置行列を
に対して
共役転置行列を
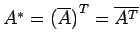 と定義する.
と定義する.
定理 5.66 (対称行列の固有値)
対称行列の固有値はすべて実数である.
を得る.ここで,
が成り立つことを用いた.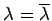 となるので,
となるので,
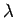 は実数である.
は実数である.
(証明)
![]() において,
において,
![]() 上の内積を用いて
上の内積を用いて
を得る.ここで,
が成り立つことを用いた.
注意 5.67 (対称行列の固有値)
実対称行列の固有値は実数なので,
固有ベクトルも実数である.
注意 5.68 (対称行列と正規行列)
対称行列は正規行列である.
定理 5.69 (対称行列の固有値)
対称行列の異なる固有値に属する固有ベクトルは直交する.
となる.
であるから,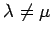 より
より
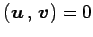 を得る.
を得る.
(証明)
対称行列は正規行列であるから固有ベクトルは直交する.
または,次のように示す.
![]() ,
,
![]() ,
,
![]() ,
,
![]() とする.
このとき,
とする.
このとき,
となる.
であるから,
定理 5.70 (対称行列の対角化)
対称行列  は
対角行列
は
対角行列 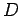 と直交行列
と直交行列  を用いて
を用いて
と対角化される.
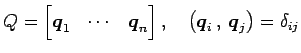 |
と対角化される.
Kondo Koichi

平成18年1月17日