5.21 演習問題 〜 対角化
問 5.56 (対角化)
次の行列  を対角化せよ.また
を対角化せよ.また 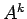 を求めよ.
を求めよ.
(1)
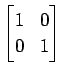 (2)
(2)
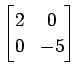 (3)
(3)
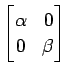 (4)
(4)
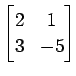 (5)
(5)
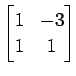
(6)
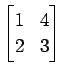 (7)
(7)
 (8)
(8)
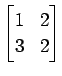 (9)
(9)
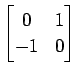 (10)
(10)
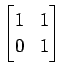
(11)
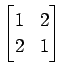 (12)
(12)
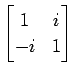 (13)
(13)
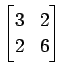 (14)
(14)
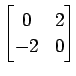 (15)
(15)
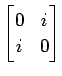
(16)
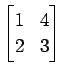 (17)
(17)
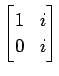 (18)
(18)
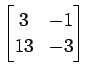 (19)
(19)
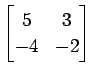 (20)
(20)
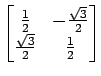
(21)
 (22)
(22)
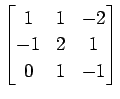 (23)
(23)
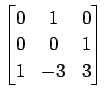 (24)
(24)
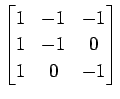
(25)
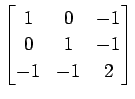 (26)
(26)
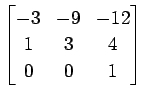 (27)
(27)
 (28)
(28)

(29)
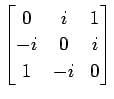 (30)
(30)
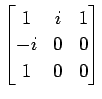 (31)
(31)
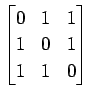 (32)
(32)

(33)
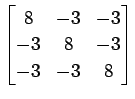 (34)
(34)
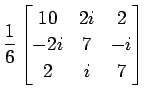 (35)
(35)
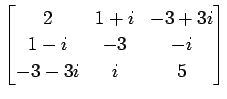
(36)
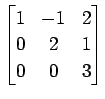 (37)
(37)
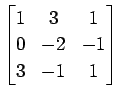 (38)
(38)
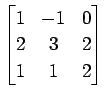 (39)
(39)
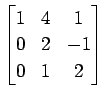
(40)
 (41)
(41)
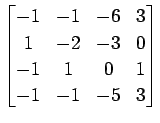 (42)
(42)
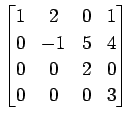
Kondo Koichi

平成18年1月17日