4.15 クラメールの公式
定理 4.88 (クラメールの方法)
連立 1 次方程式
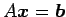 に関して,
係数行列
に関して,
係数行列
が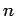 次正方行列でかつ正則なとき,
方程式の解
次正方行列でかつ正則なとき,
方程式の解
![$ \vec{x}={[ x_{1}\,\,x_{2}\,\,\cdots\,\,x_{n}]}^{T}$](img1467.png) は
は
で与えられる. これをクラメールの方法(Cramer's rule)という.
が成り立つ. 成分で表すと
より
を得る. これは第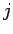 列の余因子展開だから
列の余因子展開だから
が示された.
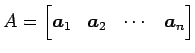 |
(803) |
が
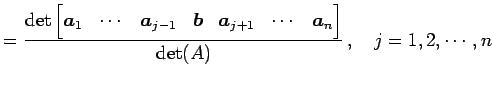 |
(804) |
で与えられる. これをクラメールの方法(Cramer's rule)という.
(証明)
![]() は正則であるから,
方程式
は正則であるから,
方程式
![]() に左から
に左から ![]() を掛けると
を掛けると
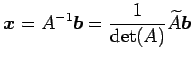 |
(805) |
が成り立つ. 成分で表すと
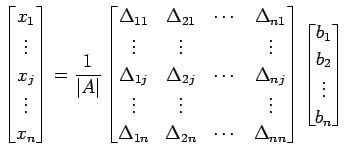 |
(806) |
より
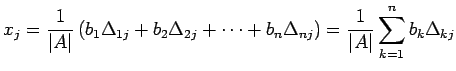 |
(807) |
を得る. これは第
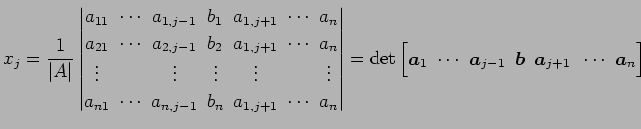 |
(808) |
が示された.
注意 4.89 (クラメールの方法)
解をもつためには分母  が 0 となってはいけない.
が 0 となってはいけない.
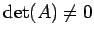 である必要がある.
すなわち
である必要がある.
すなわち  は正則のときクラメールの方法は
使用できる.
は正則のときクラメールの方法は
使用できる.
例 4.90 (クラメールの公式の使用例)
方程式
を考える. 行列式は
であり,解は
と求まる.
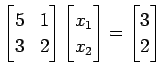 |
(809) |
を考える. 行列式は
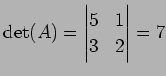 |
(810) |
であり,解は
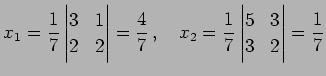 |
(811) |
と求まる.
例 4.91 (クラメールの公式の使用例)
方程式
の解を求める.
であり, 解は
である.
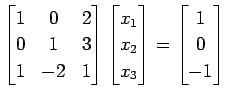 |
(812) |
の解を求める.
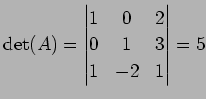 |
(813) |
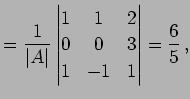
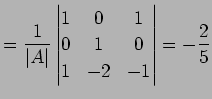
であり, 解は
 |
(814) | |
 |
(815) | |
 |
(816) |
である.
Kondo Koichi

平成17年9月15日