3.5 行列の簡約化
定義 3.20 (階段行列)
行列が
という形をしているとき, この行列を簡約な行列または 階段行列と呼ぶ. また, 各行の一番左の 0 ではない成分を主成分と呼ぶ.
![$\displaystyle \left[\begin{array}{cccccccc} \!1\! & ** & \!0\! & ** & \!0\! & *...
... \\ \vdots& & & & & & &\vdots\\ 0 &\cdots& & & & &\cdots & 0 \end{array}\right]$](img911.png) |
(428) |
という形をしているとき, この行列を簡約な行列または 階段行列と呼ぶ. また, 各行の一番左の 0 ではない成分を主成分と呼ぶ.
例 3.21 (簡約な行列の具体例)
次の行列は簡約な行列である:
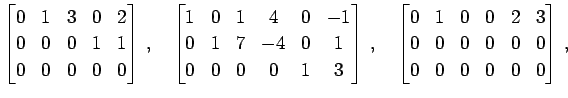 |
(429) | |
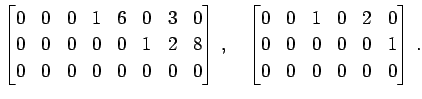 |
(430) |
定義 3.22 (簡約化)
行列  に基本変形を繰り返し,
簡約な行列
に基本変形を繰り返し,
簡約な行列  を得ることを簡約化と呼ぶ.
を得ることを簡約化と呼ぶ.
例 3.23 (簡約化の計算例)
簡約化の具体的な計算例を示す:
(1)
(2)
(3)
(4)
(1)
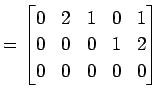 |
(431) | |
| (第一行目を |
(432) | |
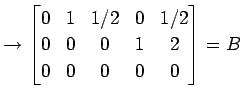 |
(433) |
(2)
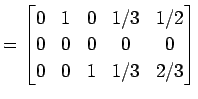 |
(434) | |
| (第二行目と第三行目を入れ替える.) | (435) | |
 |
(436) |
(3)
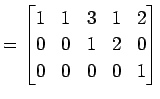 |
(437) | |
| (第二行目を |
(438) | |
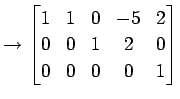 |
(439) | |
| (第三行目を |
(440) | |
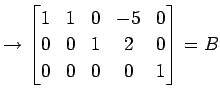 |
(441) |
(4)
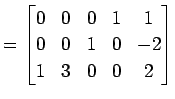 |
(442) | |
| (第一行目を第三行目を入れ替える.) | (443) | |
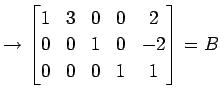 |
(444) |
定理 3.24 (簡約化の一意性)
任意の行列は基本変形により一意に簡約化できる.
Kondo Koichi

平成17年9月15日