3.4 連立方程式の解の集合
注意 3.15 (連立方程式の解の集合)
連立方程式
を考える. 第 1 式,第 2 式をみたす点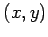 の集合は
それぞれ
の集合は
それぞれ
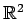 内の直線を表す.
連立方程式の解はこの 2 つの式を同時にみたす点の集合であるらか,
2 つの直線の交点が連立方程式の解となる.
交点をもつ条件は次の 3 つに分けられる.
内の直線を表す.
連立方程式の解はこの 2 つの式を同時にみたす点の集合であるらか,
2 つの直線の交点が連立方程式の解となる.
交点をもつ条件は次の 3 つに分けられる.
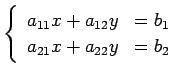 |
(417) |
を考える. 第 1 式,第 2 式をみたす点
- (i)
- 1 点で交わる場合.このとき解は一意な解と呼ぶ.
- (ii)
- 2 つの直線が重なり 1 つの直線となる場合. このとき交点は直線上のすべての点である. 解は一意には表すことができず, 任意定数を用いて表す. この解を任意定数を含む解と呼ぶことにする.
- (iii)
- 2 つの直線が平行であり,交わらない場合. このとき解なしとなる.
注意 3.16 (連立方程式の解の集合)
上の 3 つ場合となるための
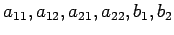 に関する条件を求めよ.
に関する条件を求めよ.
注意 3.17 (連立方程式の解の集合)
連立 1 次方程式
を考える. この方程式の解は直線上のすべての点であるから, 解が一意には定まらない. 解を具体的に書き下す. 方程式を変形すると
である. この式の右辺の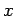 は任意の値をとることが可能である.
左辺の
は任意の値をとることが可能である.
左辺の 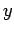 は与えられた
は与えられた 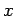 の値に応じて値が一つ定まる.
このとき解は
の値に応じて値が一つ定まる.
このとき解は
と表される. ただし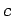 は任意の定数とする.
また解は
は任意の定数とする.
また解は
と書ける. よって解全体がなす集合は点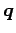 を通り
方向ベクトル
を通り
方向ベクトル 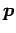 の直線となる.
また,拡大係数行列は
の直線となる.
また,拡大係数行列は
であり,掃き出し法の形には当てはまらない.
| (418) |
を考える. この方程式の解は直線上のすべての点であるから, 解が一意には定まらない. 解を具体的に書き下す. 方程式を変形すると
| (419) |
である. この式の右辺の
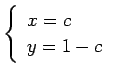 |
(420) |
と表される. ただし
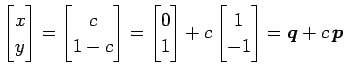 |
(421) |
と書ける. よって解全体がなす集合は点
![$\displaystyle [A\,\vert\,\vec{b}]= \left[ \begin{array}{cc\vert c} 1 & 1 & 1 \end{array}\right]$](img904.png) |
(422) |
であり,掃き出し法の形には当てはまらない.
注意 3.18 (連立方程式の解の集合)
連立方程式
を考える. 第 1 式,第 2 式,第 3 式をみたす点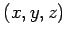 の集合は
それぞれ
の集合は
それぞれ
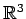 内の平面を表す.
平面の交点をもつ条件は次の 4 つに分けられる.
(i) 1 点で交わる場合.(ii) 直線となる場合.(iii) 平面となる場合.
(iv) 交点がない場合.
内の平面を表す.
平面の交点をもつ条件は次の 4 つに分けられる.
(i) 1 点で交わる場合.(ii) 直線となる場合.(iii) 平面となる場合.
(iv) 交点がない場合.
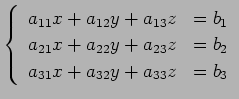 |
(423) |
を考える. 第 1 式,第 2 式,第 3 式をみたす点
注意 3.19 (連立方程式の解の集合)
連立 1 次方程式
を考える. 方程式の解を書き下す. 方程式を書き直すと
となる. 左辺には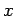 ,
, 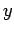 があり,
右辺は
があり,
右辺は 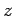 のみである.
右辺の
のみである.
右辺の 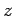 にある値が 1 つ与えらると,
その
にある値が 1 つ与えらると,
その 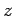 に応じて左辺の
に応じて左辺の 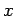 ,
, 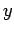 の値がそれぞれ定まる.
よって
の値がそれぞれ定まる.
よって 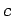 を任意の値として
を任意の値として 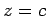 とおくと,
解は
とおくと,
解は
と表される. 解全体の集合は 3 次元空間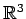 内の
点
内の
点 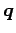 を通り方向ベクトル
を通り方向ベクトル 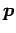 の直線である.
また,拡大係数行列は
の直線である.
また,拡大係数行列は
であり,掃き出し法の形には当てはまらない.
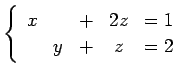 |
(424) |
を考える. 方程式の解を書き下す. 方程式を書き直すと
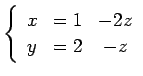 |
(425) |
となる. 左辺には
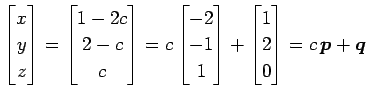 |
(426) |
と表される. 解全体の集合は 3 次元空間
![$\displaystyle [A\,\vert\,\vec{b}]= \left[ \begin{array}{ccc\vert c} 1 & 0 & 2 & 1 \\ 0 & 1 & 1 & 2 \end{array}\right]$](img910.png) |
(427) |
であり,掃き出し法の形には当てはまらない.
Kondo Koichi

平成17年9月15日