1.32
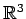 における点と平面との距離
における点と平面との距離
定理 1.138 (
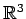 の点と平面との距離)
の点と平面との距離)
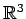 空間内の点
空間内の点
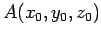 と
平面
と
平面
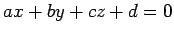 を考える.
点
を考える.
点  と平面との距離は
と平面との距離は
である.
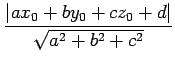 |
(245) |
である.
問 1.139 (
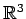 の点と平面との距離)
これを示せ.
の点と平面との距離)
これを示せ.
とおく.
より,
を得る.
(証明)
点
![]() と平面
と平面
![]() とし,
とし,
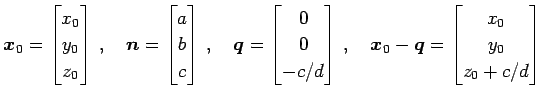 |
(246) |
とおく.
| (247) |
より,
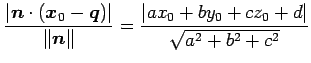 |
(248) |
を得る.
例 1.140 (
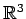 の点と平面との距離)
点
の点と平面との距離)
点 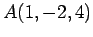 の平面
の平面
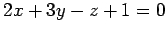 との距離は
との距離は
である.
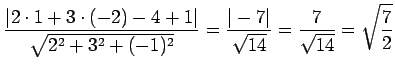 |
(249) |
である.
例 1.141 (
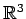 の点と平面との距離)
点
の点と平面との距離)
点 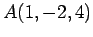 の平面
の平面
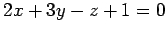 への
射影点は
への
射影点は
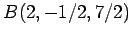 であるから
点
であるから
点  と平面との距離は点
と平面との距離は点  ,
,  の距離に等しい.
すなわち,
の距離に等しい.
すなわち,
である.
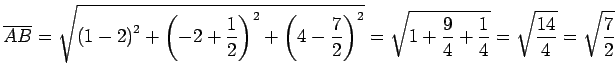 |
(250) |
である.
Kondo Koichi

平成17年9月15日