1.27 平面の方程式と連立方程式の解の一意性
例 1.123 (
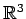 の平面の方程式の具体例)
点
の平面の方程式の具体例)
点 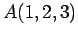 ,
, 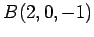 ,
,
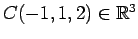 を
通る平面を考える.
平面の方程式は
を
通る平面を考える.
平面の方程式は
な形となると仮定する. 点 ,
,  ,
, 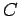 は平面上にあるので
は平面上にあるので
が成り立つ. この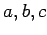 に関する連立方程式を求める.
に関する連立方程式を求める.
| (210) |
な形となると仮定する. 点
| (211) |
が成り立つ. この
注意 1.124 (
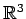 の平面の方程式と連立方程式)
平面は 3 点から一意に定まる.
これは 3 元の連立方程式は 3 本の方程式により解が
一意に定まることと等価である.
の平面の方程式と連立方程式)
平面は 3 点から一意に定まる.
これは 3 元の連立方程式は 3 本の方程式により解が
一意に定まることと等価である.
注意 1.125 (図形,次元,点,連立方程式)
| 点: | 0 次元. | |
つまり |
| 直線: | |
|
つまり |
| 平面: | |
|
つまり |
Kondo Koichi

平成17年9月15日