1.25 平面の方程式と法線ベクトル
定理 1.118 (平面の方程式)
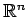 空間内の平面上の点
空間内の平面上の点 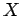 の位置ベクトルは
の位置ベクトルは
と表される.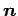 は方向ベクトル
は方向ベクトル 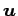 ,
, 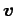 と
直交するベクトルである.
と
直交するベクトルである.
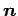 を法線ベクトル(normal vector)という.
を法線ベクトル(normal vector)という.
が成り立つ.
| (188) |
と表される.
(証明)
(
![]() )
)
![]() ,
,
![]() である.
このとき
である.
このとき
| (189) |
が成り立つ.
注意 1.119 (
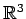 の平面の方程式)
の平面の方程式)
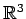 内の平面の方程式は次のように表される.
まず,基本は
内の平面の方程式は次のように表される.
まず,基本は
である. このとき,法線ベクトルは![$ \vec{n}={[a\,\,\,b\,\,c]}^{T}$](img481.png) である.
また,この式を変形して
である.
また,この式を変形して
と表す.このとき, 法線ベクトルは![$ \vec{n}={[a\,\,\,b\,\,c]}^{T}$](img481.png) であり,
平面は点
であり,
平面は点
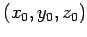 を通る.
さらに変形して,
を通る.
さらに変形して,
とする.このとき平面と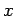 軸,
軸,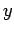 軸,
軸,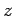 軸との
交点はそれぞれ
軸との
交点はそれぞれ 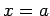 ,
, 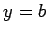 ,
, 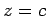 となる.
となる.
| (190) |
である. このとき,法線ベクトルは
| (191) |
と表す.このとき, 法線ベクトルは
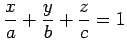 |
(192) |
とする.このとき平面と
例 1.120 (
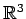 の平面の方程式の具体例)
の平面の方程式の具体例)
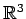 内の平面の方程式
内の平面の方程式
を考える. 法線ベクトルは![$ \vec{n}={[1\,\,\,-2\,\,3]}^{T}$](img489.png) である.
また,方程式を変形して
である.
また,方程式を変形して
を得る. 平面は点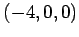 ,
, 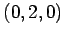 ,
,
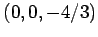 を通る.
を通る.
| (193) |
を考える. 法線ベクトルは
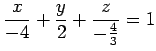 |
(194) |
を得る. 平面は点
Kondo Koichi

平成17年9月15日