1.23
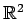 における点と直線との距離
における点と直線との距離
定理 1.112 (
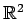 内の点と直線の距離)
内の点と直線の距離)
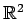 空間内の点
空間内の点
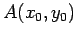 と
直線
と
直線 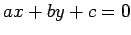 との距離は
との距離は
である.
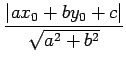 |
(175) |
である.
問 1.113 (
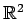 内の点と直線の距離)
これを示せ.
内の点と直線の距離)
これを示せ.
とおくと
である.よって距離は
である.
(証明)
![]() 空間を
空間を
![]() 空間内の部分空間として考える.
このとき,点
空間内の部分空間として考える.
このとき,点
![]() と直線
と直線
![]() を考える.
を考える.
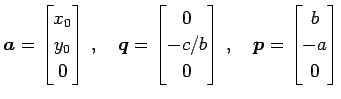 |
(176) |
とおくと
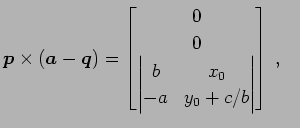 |
(177) | |
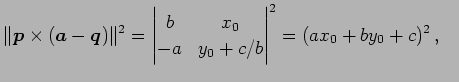 |
(178) | |
| (179) |
である.よって距離は
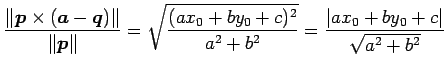 |
(180) |
である.
問 1.114 (
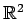 内の点と直線の距離)
点
内の点と直線の距離)
点 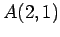 と直線
と直線 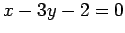 との距離は
との距離は
である.
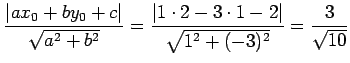 |
(181) |
である.
Kondo Koichi

平成17年9月15日