1.22
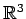 における点と直線との距離
における点と直線との距離
定理 1.109 (点と直線の距離)
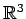 空間内の
点
空間内の
点  と直線
と直線
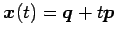 との距離は
との距離は
である.
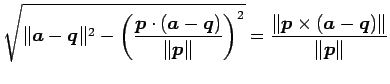 |
(165) |
である.
問 1.110 (
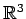 内の点と直線の距離)
これを示せ.
内の点と直線の距離)
これを示せ.
となる. ここで
を用いると
となり定理を得る.
と表される.また点 と直線の距離を
と直線の距離を 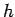 とする.
このとき
とする.
このとき 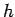 は三角形
は三角形 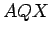 の高さを意味する.
よって
の高さを意味する.
よって
が成り立つ. 以上より
を得る.
(証明その1)
距離
![]() は
は
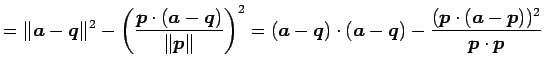 |
(166) | |
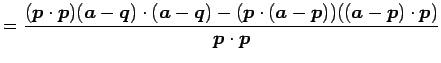 |
(167) |
となる. ここで
| (168) |
を用いると
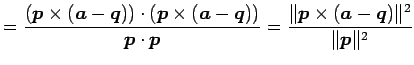 |
(169) |
となり定理を得る.
(証明その2)
![]() 点
点
![]() ,
,
![]() ,
,
![]() からなる
三角形
からなる
三角形 ![]() を考える.
三角形の面積は外積の定義より
を考える.
三角形の面積は外積の定義より
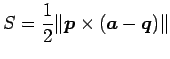 |
(170) |
と表される.また点
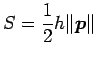 |
(171) |
が成り立つ. 以上より
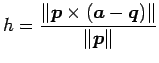 |
(172) |
を得る.
例 1.111 (
 内の点と直線の距離)
点
内の点と直線の距離)
点  と直線
と直線
![$ \vec{x}(t)={[1\,\,\,3\,\,-1]}^{T}+t{[2\,\,-1\,\,1]}^{T}$](img422.png) との
距離を考える.
との
距離を考える.
より,距離は
である.
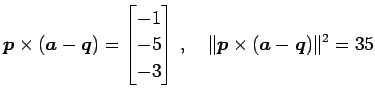 |
(173) |
より,距離は
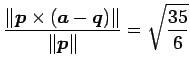 |
(174) |
である.
Kondo Koichi

平成17年9月15日