1.9 内積
定義 1.47 (内積)
![$ \mathbb{R}^{n}\ni\vec{a}={[a_{1}\,\,a_{2}\,\,\cdots\,\,a_{n}]}^{T}$](img228.png) ,
,
![$ \vec{b}={[b_{1}\,\,b_{2}\,\,\cdots\,\,b_{n}]}^{T}$](img229.png) に対して
に対して
なる二項演算を内積(inner product)または スカラー積(scalar product)という. また,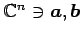 に対しては
に対しては
と定義する.
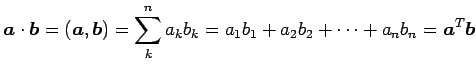 |
(64) |
なる二項演算を内積(inner product)または スカラー積(scalar product)という. また,
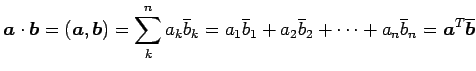 |
(65) |
と定義する.
例 1.48 (内積の具体例)
ベクトル
の内積は
である.
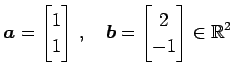 |
(66) |
の内積は
| (67) |
である.
例 1.49 (内積の具体例)
ベクトル
の内積は
である.
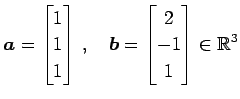 |
(68) |
の内積は
| (69) |
である.
例 1.50 (内積の具体例)
ベクトル
の内積は
である.
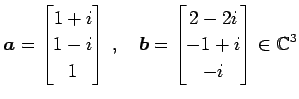 |
(70) |
の内積は
| (71) |
である.
定理 1.51 (内積の性質)
- (i)
-
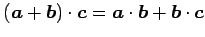
- (ii)
-
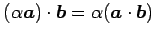
- (iii)
-
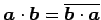
- (iv)
-
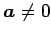 のとき
のとき
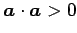
問 1.52 (内積の性質)
これを示せ.
Kondo Koichi

平成17年9月15日