3.13 多重積分の広義積分への応用
例 3.63 (多重積分の広義積分への応用)
広義積分
を求める. 関数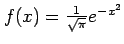 を
誤差関数またはガウシアン(Gaussian)といい,
正規分布関数に用いられる.
を
誤差関数またはガウシアン(Gaussian)といい,
正規分布関数に用いられる.
とおき,多重積分
を考える.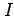 を計算すると
を計算すると
となる.ここで,
である.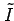 を計算すると
を計算すると
となる.
があり, 領域の面積には
と大小関係がある. 同じ正の関数に対する異なる領域での多重積分は, 領域の面積が大きい方が多重積分の値は大きくなる. よって,
が成り立つ. これは先ほどの計算結果より
となる.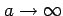 の極限をとるとはさみうちの定理より,
の極限をとるとはさみうちの定理より,
を得る.よって,
が成り立つ.
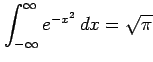 |
を求める. 関数
まず,円の内部の領域 ![]() と正方形の領域
と正方形の領域 ![]() を
を
とおき,多重積分
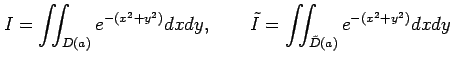 |
を考える.
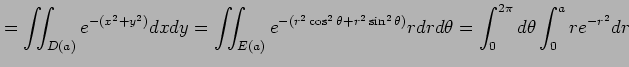 |
||
![$\displaystyle = \left(\int_0^{2\pi}d\theta\right) \left(\int_0^{a}re^{-r^2}dr\r...
...1.5em width0em depth0.1em\,{-\frac{1}{2}e^{-r^2}}\,\right]_0^a= \pi(1-e^{-a^2})$](img1630.png) |
となる.ここで,
である.
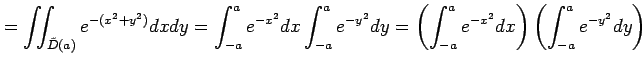 |
||
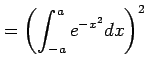 |
となる.
次に,領域 ![]() ,
,
![]() ,
,
![]() を考える.
これらは下図 (b) のように包含関係
を考える.
これらは下図 (b) のように包含関係
があり, 領域の面積には
と大小関係がある. 同じ正の関数に対する異なる領域での多重積分は, 領域の面積が大きい方が多重積分の値は大きくなる. よって,
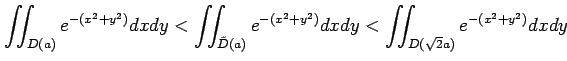 |
が成り立つ. これは先ほどの計算結果より
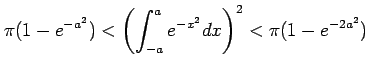 |
となる.
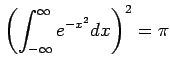 |
を得る.よって,
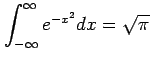 |
が成り立つ.
![\includegraphics[width=0.45\textwidth]{gauss-f.eps}](img1647.png) |
![\includegraphics[width=0.45\textwidth]{gauss-D.eps}](img1648.png) |
| (a) |
(b) 領域 |
Kondo Koichi

平成18年1月18日