1.1
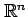 の直線
の直線
定義 1.1 (位置ベクトル)
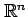 の空間の点
の空間の点
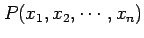 に対して,
列ベクトル
に対して,
列ベクトル
を点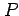 の位置ベクトル(position vector)という.
点
の位置ベクトル(position vector)という.
点 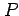 とベクトル
とベクトル 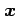 を同一視する.
を同一視する.
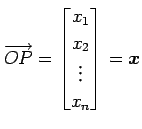 |
を点
定義 1.2 (直線)
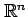 の点
の点 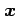 がパラメータ
がパラメータ
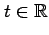 を用いて
を用いて
と表されるとする. このとき点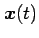 の軌跡を直線(line)という.
の軌跡を直線(line)という.
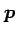 を方向ベクトル(direction vector)という.
を方向ベクトル(direction vector)という.
と表されるとする. このとき点
定理 1.3 (内分点)
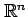 の点
の点 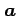 ,
, 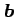 を通る直線をむすび,
その直線上の点で
点
を通る直線をむすび,
その直線上の点で
点 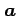 ,
, 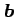 からの
距離の比が
からの
距離の比が 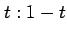 となる点
となる点 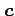 は
は
で与えられる.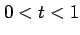 のとき点
のとき点 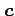 を 点
を 点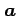 ,
, 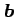 の
内分点(internally dividing point)といい,
の
内分点(internally dividing point)といい,
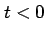 ,
, 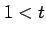 のとき
外分点(externally dividing point)という.
のとき
外分点(externally dividing point)という.
で与えられる.
定義 1.4 (直線)
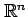 の点
の点 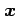 がパラメータ
がパラメータ
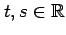 を用いて
を用いて
と表されるとする. このとき点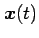 の軌跡を平面(plane)という.
の軌跡を平面(plane)という.
と表されるとする. このとき点
Kondo Koichi

平成18年1月18日