5.3 テイラー級数の導出
巾級数
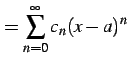 |
(568) |
を考える. 関数
まず巾級数
| (569) |
に
| (570) |
となる.よって係数を
| (571) |
となる. 両辺を微分すると
| (572) |
を得る.ここに
| (573) |
となるので係数を
| (574) | ||
| (575) |
となる. これで
| (576) | ||
| (577) | ||
| (578) | ||
| (579) |
となる.
| (580) | ||
| (581) | ||
| (582) | ||
| (583) |
となるので係数が
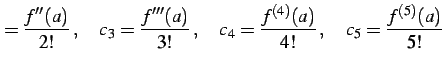 |
(584) |
と定まる. 同様な操作を繰り返せば
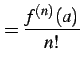 |
(585) |
を得る.
Kondo Koichi

平成17年8月31日