5.2 テイラー級数
巾級数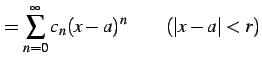 |
(559) | |
| (560) |
とおく. 数列
| 数列: |
(561) |
との対応関係がある. それでは関数
| 関数: |
(562) |
を考える.
定理 5.6 (テイラー級数)
関数  が
が 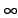 回微分可能なとき,
回微分可能なとき,
が成り立つ. ただし点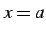 は定義内のある点とする.
この巾級数を関数
は定義内のある点とする.
この巾級数を関数  に関する
に関する 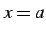 まわりの
テイラー級数(Taylor series)と呼ぶ.
特に
まわりの
テイラー級数(Taylor series)と呼ぶ.
特に 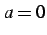 のときは,
マクローリン級数(Maclaurin series)と呼ぶ.
のときは,
マクローリン級数(Maclaurin series)と呼ぶ.
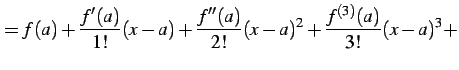 |
(563) | |
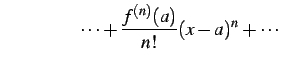 |
(564) | |
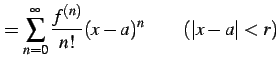 |
(565) |
が成り立つ. ただし点
注意 5.7 (テイラー級数の収束半径)
テイラー級数は巾級数
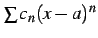 を
を
とおいたものである. よってテイラー級数の収束半径は
により求まる.
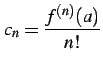 |
(566) |
とおいたものである. よってテイラー級数の収束半径は
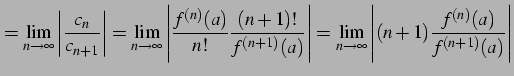 |
(567) |
により求まる.
Kondo Koichi

平成17年8月31日