4.11 等比数列
例 4.36 (等比級数)
等比数列
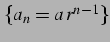 の無限和を
等比級数(geometrical progression series)と呼び,
の無限和を
等比級数(geometrical progression series)と呼び,
と書き表す. 等比級数は
となる.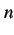 部分和
部分和
を考える.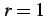 のとき,
のとき,
となる. つぎに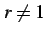 のとき,等式
のとき,等式
を用いると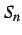 は
は
と書ける. 以上より
となる. ただし無限大の符号は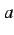 の符号
の符号
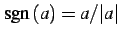 で決まる.
証明終り.
で決まる.
証明終り.
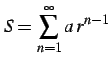 |
(462) |
と書き表す. 等比級数は
![$\displaystyle S=\left\{ \begin{array}{ll} \displaystyle{\frac{a}{1-r}} & (\vert r\vert< 1) \\ [1em] \text{発散} & (\vert r\vert\ge 1) \end{array} \right.$](img1092.png) |
(463) |
となる.
(証明) 第
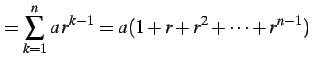 |
(464) |
を考える.
| (465) |
となる. つぎに
| (466) |
を用いると
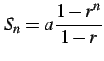 |
(467) |
と書ける. 以上より
![$\displaystyle S=\lim_{n\to\infty}S_{n}= \left\{ \begin{array}{lc} \displaystyle...
...& (-1<r<1)\\ [2ex] \displaystyle{\text{不確定}} & (r\leq-1) \end{array} \right.$](img1099.png) |
(468) |
となる. ただし無限大の符号は
問 4.37 (1を根にもつ多項式の因数分解)
次の等式を示せ.
| (469) |
注意 4.38 (初項が異なる級数)
級数が
と定義されるときの値を考える. 部分和は
となるから, 結局級数は
と得られる.
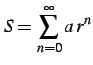 |
(470) |
と定義されるときの値を考える. 部分和は
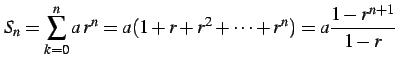 |
(471) |
となるから, 結局級数は
![$\displaystyle S= \lim_{n\to\infty}S_{n}= \lim_{n\to\infty}a\frac{1-r^{n+1}}{1-r...
...(\vert r\vert<1) \\ [1ex] \text{発散} & (\vert r\vert\geq1) \end{array} \right.$](img1104.png) |
(472) |
と得られる.
注意 4.39 (等比級数の有理式表現)
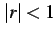 のとき
のとき
となる. この式は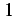 を
を 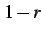 で割ることでも導出される.
すなわち,
で割ることでも導出される.
すなわち,
のように低次項を主項として割り算を無限回続ける.
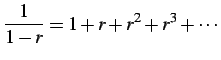 |
(473) |
となる. この式は
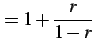 |
(474) | |
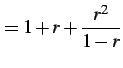 |
(475) | |
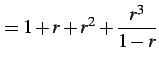 |
(476) | |
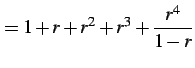 |
(477) | |
| (478) |
のように低次項を主項として割り算を無限回続ける.
例 4.40 (等比級数の具体例)
または
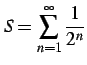 |
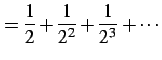 |
(479) |
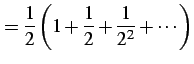 |
(480) | |
| (481) | ||
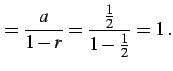 |
(482) |
または
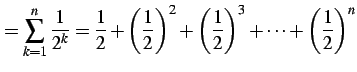 |
(483) | |
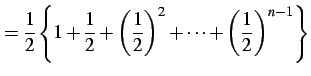 |
(484) | |
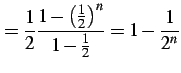 |
(485) |
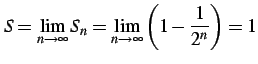 |
(486) |
例 4.41 (等比級数の具体例)
または
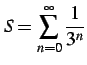 |
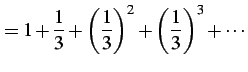 |
(487) |
| (488) | ||
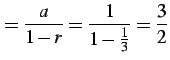 |
(489) |
または
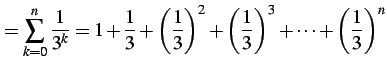 |
(490) | |
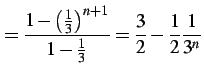 |
(491) |
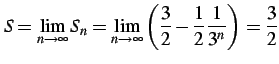 |
(492) |
例 4.42 (等比級数の具体例)
| (493) |
(証明)
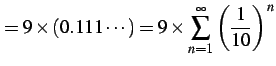 |
(494) | |
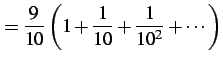 |
(495) | |
| (496) | ||
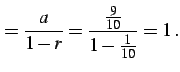 |
(497) |
問 4.43 (級数の計算)
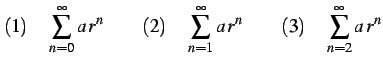 |
(498) | |
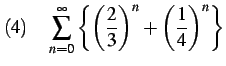 |
(499) | |
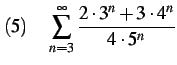 |
(500) |
Kondo Koichi

平成17年8月31日