4.9 数列の有界性と単調性
定義 4.26 (有界数列)
数列 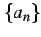 に対して次の性質を定義する.
に対して次の性質を定義する.
-
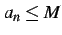 を満たすとき,
数列
を満たすとき,
数列  は上に有界(bounded from above)
であるという.
は上に有界(bounded from above)
であるという.
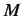 を上界(upper bound)と呼ぶ.
を上界(upper bound)と呼ぶ.
-
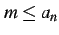 を満たすとき,
数列
を満たすとき,
数列 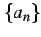 は
下に有界(bounded from below)であるという.
は
下に有界(bounded from below)であるという.
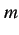 を下界(lower bound)と呼ぶ.
を下界(lower bound)と呼ぶ.
-
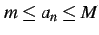 を満たすとき,
数列
を満たすとき,
数列 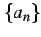 は有界(bounded)であるという.
は有界(bounded)であるという.
例 4.27 (有界な数列の具体例)
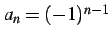 は
は
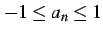 を満たすので有界である.
を満たすので有界である.
定義 4.28 (単調数列)
数列 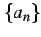 に対して次の性質を定義する.
に対して次の性質を定義する.
-
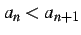 を満たすとき,
数列
を満たすとき,
数列 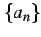 は
単調増加(monotonic increasing)であるという.
は
単調増加(monotonic increasing)であるという.
-
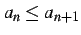 を満たすとき,
数列
を満たすとき,
数列 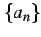 は
広義の単調増加
(monotonic increasing in the wider sense)であるという.
は
広義の単調増加
(monotonic increasing in the wider sense)であるという.
-
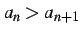 を満たすとき,
数列
を満たすとき,
数列 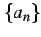 は
単調減少(monotonic decreasing)であるという.
は
単調減少(monotonic decreasing)であるという.
-
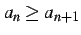 を満たすとき,
数列
を満たすとき,
数列 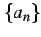 は
広義の単調減少(monotonic decreasing in the wider sense)で
あるという.
は
広義の単調減少(monotonic decreasing in the wider sense)で
あるという.
定理 4.29 (有界な単調数列の収束性)
有界な広義の単調数列は収束する.
例 4.30 (有界な単調数列の具体例)
数列
を考える.
を満たすので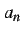 は単調増加である.
初項
は単調増加である.
初項
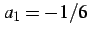 は下界となる.
上界は
は下界となる.
上界は
により求まる.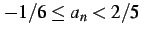 となるので
となるので 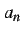 は有界である.
定理より
は有界である.
定理より 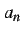 は収束する.
実際,極限を求めると
は収束する.
実際,極限を求めると
と得られる.
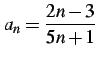 |
(444) |
を考える.
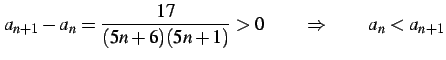 |
(445) |
を満たすので
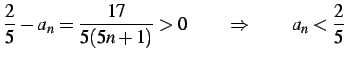 |
(446) |
により求まる.
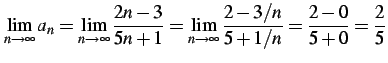 |
(447) |
と得られる.
Kondo Koichi

平成17年8月31日