4.6 収束する数列のいろいろ
例 4.20 (有理式で表される数列の極限)
一般項が
により与えられる数列を考える. 定理を適用して計算を試みる. 分子分母の極限をとり,
を得るがこれは誤りである. そもそも分子分母はそれぞれ発散するので定理は適用不可である. あらためて計算を行なう:
今回は有限確定となり極限が求まる. 計算の途中においては,定理が適用可能であるかの判断は難しい. 最終形まで計算した結果が有限確定または無限確定であれば, 途中の計算も定理が適用可能であることが多い.
で与えられる数列を考える.式を変形して極限を考える:
である数列の極限を考える. 式を変形して極限を考える:
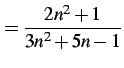 |
(419) |
により与えられる数列を考える. 定理を適用して計算を試みる. 分子分母の極限をとり,
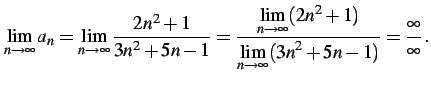 ←不確定 ←不確定 |
(420) |
を得るがこれは誤りである. そもそも分子分母はそれぞれ発散するので定理は適用不可である. あらためて計算を行なう:
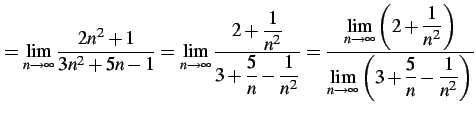 |
(421) | |
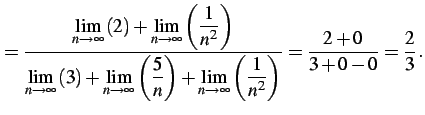 ←有限確定 ←有限確定 |
(422) |
今回は有限確定となり極限が求まる. 計算の途中においては,定理が適用可能であるかの判断は難しい. 最終形まで計算した結果が有限確定または無限確定であれば, 途中の計算も定理が適用可能であることが多い.
次に一般項が
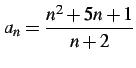 |
(423) |
で与えられる数列を考える.式を変形して極限を考える:
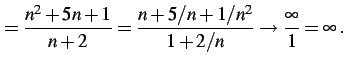 ←無限確定 ←無限確定 |
(424) |
最後に一般項が
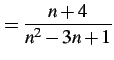 |
(425) |
である数列の極限を考える. 式を変形して極限を考える:
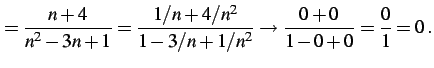 ←有限確定 ←有限確定 |
(426) |
以上をまとめると, 有理式で表される数列の極限は, 有理式の最大次数の巾で分子分母を割った後に極限をとればよい.
例 4.21 (根号を含む数列の極限)
一般項が
で与えられる数列の極限を考える. 式を次のように変形した後に極限をとる:
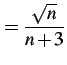 |
(427) |
で与えられる数列の極限を考える. 式を次のように変形した後に極限をとる:
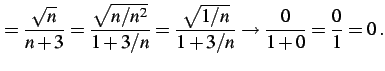 |
(428) |
Kondo Koichi

平成17年8月31日