3.10 実数巾の巾関数の微分
定理 3.23 (巾関数の微分)
と表されるのでこれを微分すると
を得る.
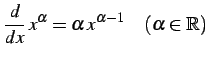 |
(263) |
(証明)
![]() と
と
![]() は証明済みである.
これを用いて証明をする.
このとき
は証明済みである.
これを用いて証明をする.
このとき
| (264) |
と表されるのでこれを微分すると
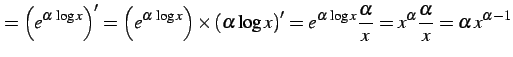 |
(265) |
を得る.
Kondo Koichi

平成17年8月31日