3.9 指数関数の微分
定理 3.21 (指数関数の微分)
関数 | (259) | ||
| (260) |
問 3.22
これを示せ.
である.これと逆関数の微分公式より
を得る.
(証明)
![]() とおく.
このとき逆関数とその微分は
とおく.
このとき逆関数とその微分は
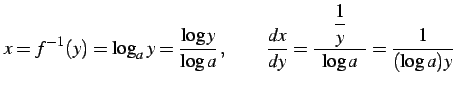 |
(261) |
である.これと逆関数の微分公式より
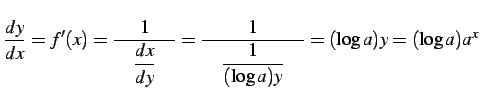 |
(262) |
を得る.
Kondo Koichi

平成17年8月31日