2.23 関数の極限
定義 2.72 (右極限,左極限)
変数 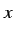 を右から
を右から 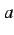 に近づけたときの
に近づけたときの  の値が
の値が 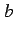 に近づくとき
に近づくとき
と書き,右極限(right-hand limit)と呼ぶ. 同様に, 変数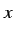 を左から
を左から 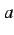 に近づけたときの
に近づけたときの  の値が
の値が 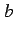 に近づくとき
に近づくとき
と書き,左極限(left-hand limit)と呼ぶ.
と書くこともある.
| (130) |
と書き,右極限(right-hand limit)と呼ぶ. 同様に, 変数
| (131) |
と書き,左極限(left-hand limit)と呼ぶ.
また略記として
| (132) |
と書くこともある.
定義 2.73 (関数の極限)
変数 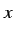 を
を 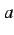 に近づけるとき,
その近づけ方に依らず全て同じ極限となるとき,
すなわち
に近づけるとき,
その近づけ方に依らず全て同じ極限となるとき,
すなわち
が成り立つとき, そのときに限り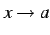 における関数
における関数  の極限が存在し,
の極限が存在し,
と書く. 極限が存在するとき次のように表現する:
収束しないとき発散する(divergent)という.
| (133) |
が成り立つとき, そのときに限り
と書く. 極限が存在するとき次のように表現する:
| 関数 |
(135) | |
| (136) | ||
| (137) | ||
| (138) |
収束しないとき発散する(divergent)という.
例 2.74 (関数の極限の具体例)
関数 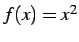 を考える.
このとき
を考える.
このとき
となる. 右からの極限も左からの極限も存在し同じ値となる. よって
である.
| (139) |
となる. 右からの極限も左からの極限も存在し同じ値となる. よって
| (140) |
である.
例 2.75 (関数の極限の具体例)
関数
を考える.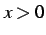 のとき
のとき
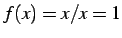 であるから
右極限は
であるから
右極限は
となる.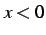 のとき
のとき
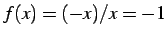 であるから
左極限は
であるから
左極限は
となる. 右極限と左極限が一致しないので, 極限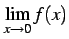 は存在しない.
は存在しない.
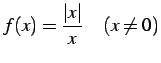 |
(141) |
を考える.
| (142) |
となる.
| (143) |
となる. 右極限と左極限が一致しないので, 極限
例 2.76 (関数の極限の具体例)
関数
を考える.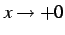 のとき
のとき
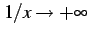 である.
である.
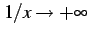 であるから
であるから  は
は 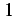 と
と 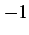 の間を振動する.
よって右極限
の間を振動する.
よって右極限
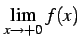 は存在しない.
は存在しない.
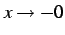 のとき
のとき
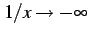 である.
以下同様で左極限
である.
以下同様で左極限
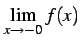 は存在しない.
右極限も左極限も存在しないので,
極限
は存在しない.
右極限も左極限も存在しないので,
極限
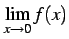 は存在しない.
は存在しない.
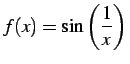 |
(144) |
を考える.
Kondo Koichi

平成17年8月31日