2.7 逆関数
定義 2.23 (逆関数)
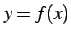 を方程式とみなし,
を方程式とみなし,
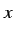 について解いたとき
について解いたとき 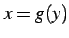 が得られたとする.
このとき
が得られたとする.
このとき 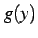 を逆関数(inverse function)
と呼び
を逆関数(inverse function)
と呼び
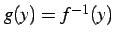 と書く.
変数の表し方が本質的でない場合は
と書く.
変数の表し方が本質的でない場合は
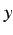 と
と 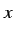 を取り替えて
を取り替えて 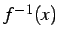 と書く.
と書く.
注意 2.24 (逆関数)
逆関数の定義より明らかに
が成り立つ. これは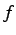 を写像と考えれば
を写像と考えれば
と表される.
| (38) |
が成り立つ. これは
| (39) |
と表される.
例 2.25 (逆関数の具体例)
関数
の逆関数を考える.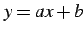 について解くと,
について解くと,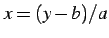 となるので,
逆関数は
となるので,
逆関数は
となる.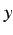 と
と 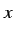 を入れ替えると
を入れ替えると
である.
| (40) |
の逆関数を考える.
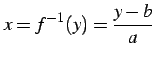 |
(41) |
となる.
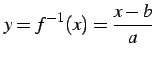 |
(42) |
である.
例 2.26 (逆関数の具体例)
関数
の逆関数は
である.
| (43) |
の逆関数は
| (44) |
である.
例 2.27 (逆関数の具体例)
関数 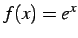 の逆関数は
の逆関数は
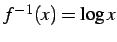 であり,
であり,
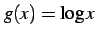 の逆関数は
の逆関数は
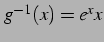 である.
である.
問 2.28 (逆関数のグラフ)
関数 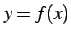 のグラフとその逆関数
のグラフとその逆関数
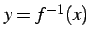 のグラフは,
直線
のグラフは,
直線 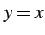 に関して線対称である.
これを示せ.
に関して線対称である.
これを示せ.
Kondo Koichi

平成17年8月31日