2.6 関数

次: 2.7 逆関数上: 2 関数前: 2.5 逆写像

2.6 関数

関数（function）とは，ある値が与えられたとき，何らかの演算規則に従って値を定め，その値を返す機能のことである．関数は

$\displaystyle y=f(x)$ (32)

と書き表される．例えばある関数をと書くことにすると，

$\displaystyle f(1)$ $\displaystyle =1^3-2\times1+5=4\,x$ $\displaystyle \to$ $\displaystyle y$ $\displaystyle =4$ (33)

$\displaystyle f(0)$ $\displaystyle =0^3-2\times0+5=5\,$ $\displaystyle \to$ $\displaystyle y$ $\displaystyle =5$ (34)

$\displaystyle f(-2)$ $\displaystyle =(-2)^3-2\times(-2)+5=1\,$ $\displaystyle \to$ $\displaystyle y$ $\displaystyle =1$ (35)

$\displaystyle f(a)$ $\displaystyle =a^3-2a+5\,$ $\displaystyle \to$ $\displaystyle y$ $\displaystyle =a^3-2a+5\,$ (36)

のように，の左辺の括弧内のがある数に書き置き換われば，右辺のもその数に置き換わる．そしてそれぞれのに応じて値が定まる．
入力にある変換を作用させ出力を返す．これを

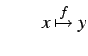$\displaystyle f:x\mapsto y$ または $\displaystyle \qquad x\overset{f}{\mapsto} y$ (37)

と表す．

定義 2.20 (関数に関する名称) 関数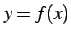に関連して次の名称を定義する：

定数（constant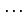） $\cdots$ 一定の値を表す数．

変数（variable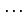） $\cdots$ 変化する値を表す数．

独立変数（independent variable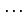） $\cdots$ 自由に値を定めることができる変数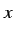のこと．

従属変数（dependent variable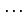） $\cdots$ 独立変数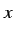に応じて値が変化する変数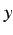のこと．

定義域，変域（domain） $\cdots$ 独立変数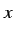がとり得る範囲．

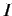値域（range） $\cdots$ 従属変数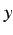がとり得る範囲．

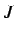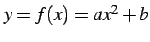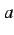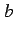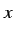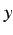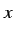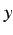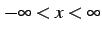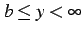例 2.21 (関数に関する名称の具体例) 関数を考える．このとき , は定数であり，, は変数である．または独立変数であり，は従属変数である．定義域は $-\infty<x<\infty$ であり，値域は $b\le y<\infty$ である．

定義 2.22 (グラフ) 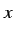軸と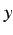軸を直角に交わるように描き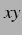平面を用意する．変数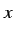の値を定義域内で変化させ，点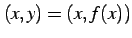の軌跡を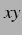平面内に描く．この曲線を関数のグラフ（graph）と呼ぶ．

次: 2.7 逆関数上: 2 関数前: 2.5 逆写像

Kondo Koichi
平成17年8月31日

$\displaystyle f(1)$	$\displaystyle =1^3-2\times1+5=4\,x$	$\displaystyle \to$	$\displaystyle y$	$\displaystyle =4$	(33)
$\displaystyle f(0)$	$\displaystyle =0^3-2\times0+5=5\,$	$\displaystyle \to$	$\displaystyle y$	$\displaystyle =5$	(34)
$\displaystyle f(-2)$	$\displaystyle =(-2)^3-2\times(-2)+5=1\,$	$\displaystyle \to$	$\displaystyle y$	$\displaystyle =1$	(35)
$\displaystyle f(a)$	$\displaystyle =a^3-2a+5\,$	$\displaystyle \to$	$\displaystyle y$	$\displaystyle =a^3-2a+5\,$	(36)