2.4 恒等写像
定義 2.14 (恒等写像)
写像 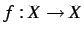 において
において 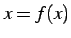 をみたすとき,
すなわち
をみたすとき,
すなわち 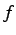 が変化をおよぼさない変換であるとき,
が変化をおよぼさない変換であるとき,
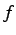 を恒等写像(identity mapping)といい,
を恒等写像(identity mapping)といい,
と表記する.
| (30) |
と表記する.
例 2.15 (恒等写像の具体例)
写像
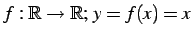 は恒等写像である.
は恒等写像である.
Kondo Koichi

平成17年8月31日
2.4 恒等写像
定義 2.14 (恒等写像) 写像において
をみたすとき, すなわち
が変化をおよぼさない変換であるとき,
を恒等写像(identity mapping)といい,
(30)
と表記する.
例 2.15 (恒等写像の具体例) 写像は恒等写像である.
Kondo Koichi


平成17年8月31日