2.3 合成写像
定義 2.11 (合成写像)
写像
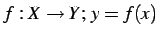 と
と
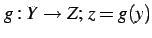 に対して
に対して
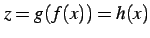 により定まる写像
により定まる写像 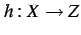 を
を
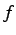 と
と 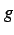 の合成写像(composite)といい,
の合成写像(composite)といい,
と表記する.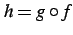 は合成関数ともいう.
は合成関数ともいう.
| (27) |
と表記する.
例 2.12 (合成写像の具体例)
写像
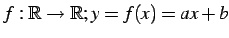 と
と
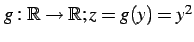 の合成写像は
の合成写像は
である.
| (28) |
である.
定理 2.13 (合成写像の性質)
写像の合成に対して結合則
が成り立つ.
| (29) |
が成り立つ.
Kondo Koichi

平成17年8月31日