6.18 コーシーの主値積分
定義 6.71 (コーシーの主値積分)
関数  が
が 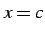
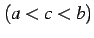 で不連続で,
有限区間
で不連続で,
有限区間 ![$ [a,b]$](img2002.png) で連続なとき,
で連続なとき,
を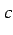 におけるコーシーの主値積分(Cauchy's principal values
of integral)という.
また関数
におけるコーシーの主値積分(Cauchy's principal values
of integral)という.
また関数  が無限区間
が無限区間
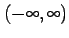 で連続なとき,
で連続なとき,
を におけるコーシーの主値積分という.
主値積分はまた
におけるコーシーの主値積分という.
主値積分はまた
とも表記する.
v.p.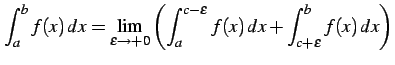 |
(1136) |
を
v.p.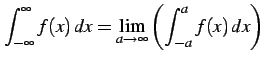 |
(1137) |
を
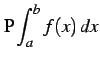 |
(1138) |
とも表記する.
例 6.72 (広義積分での計算例)
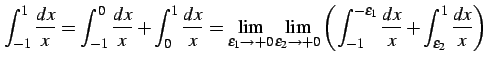 |
(1139) | |
![$\displaystyle = \lim_{\varepsilon_{1}\to+0} \Big[\log\vert x\vert\Big]_{-1}^{-\...
...}+ \lim_{\varepsilon_{2}\to+0} \Big[\log\vert x\vert\Big]_{\varepsilon_{2}}^{1}$](img2165.png) |
(1140) | |
| (1141) | ||
| (1142) |
例 6.73 (コーシーの主値積分での計算例)
v.p.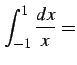 v.p. v.p.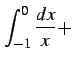 v.p. v.p.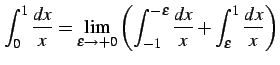 |
(1143) | |
![$\displaystyle = \lim_{\varepsilon\to+0} \Big[\log\vert x\vert\Big]_{-1}^{-\varepsilon}+ \Big[\log\vert x\vert\Big]_{\varepsilon}^{1}$](img2171.png) |
(1144) | |
| (1145) | ||
| (1146) |
Kondo Koichi

平成17年8月31日