6.15 曲線の長さ
定理 6.54 (曲線の長さ)
区間 ![$ [a,b]$](img2002.png) における関数
における関数 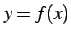 のグラフの曲線の長さは
のグラフの曲線の長さは
により得られる.
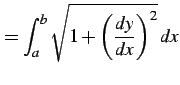 |
(1095) |
により得られる.
注意 6.55 (曲線の長さ)
曲線 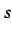 のうちある点
のうちある点 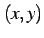 のまわりの微小線分を
のまわりの微小線分を 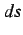 とする.
このとき
とする.
このとき 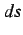 を斜辺とする直角三角形を考える.
その他の辺の長さを
を斜辺とする直角三角形を考える.
その他の辺の長さを 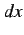 ,
, 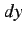 とするとピタゴラスの定理より
とするとピタゴラスの定理より
が成り立つ. 数学的には厳密ではないが次の展開をすると微小線分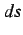 は
は
と表される. 曲線の長さ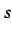 は微小線分
は微小線分 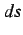 を全て足し合わせたものだから
を全て足し合わせたものだから
となる.
| (1096) |
が成り立つ. 数学的には厳密ではないが次の展開をすると微小線分
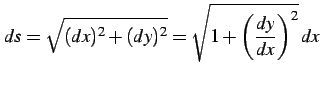 |
(1097) |
と表される. 曲線の長さ
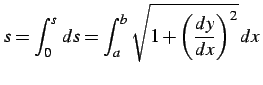 |
(1098) |
となる.
例 6.56 (曲線の長さの計算例)
単位円の円周の長さを考える.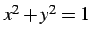 より
より
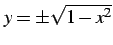 だから
多価関数の枝を分けて
だから
多価関数の枝を分けて
とする.このとき
が成り立つ.よって
を得る.
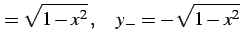 |
(1099) |
とする.このとき
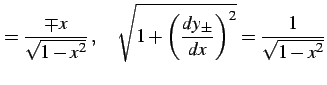 |
(1100) |
が成り立つ.よって
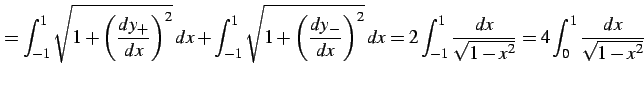 |
(1101) | |
![$\displaystyle = 4\Big[\mathrm{Sin}^{-1}x\Big]_{0}^{1}= 4\left(\mathrm{Sin}^{-1}(1)-\mathrm{Sin}^{-1}(0)\right)= 4\left(\frac{\pi}{2}-0\right)=2\pi$](img2110.png) |
(1102) |
を得る.
例 6.57 (曲線の長さの計算例)
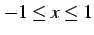 における曲線
における曲線 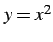 の長さ考える.
の長さ考える.
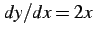 であるから曲線の長さ
であるから曲線の長さ 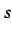 は
は
と表される.積分を計算する.置換積分として
とおく.すると
となる.双曲線関数の性質
を用いると
となる.
を用いると
となる.ここで
であることを用いると
を得る.
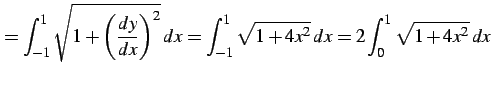 |
(1103) |
と表される.積分を計算する.置換積分として
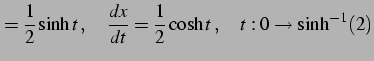 |
(1104) |
とおく.すると
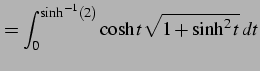 |
(1105) |
となる.双曲線関数の性質
| (1106) |
を用いると
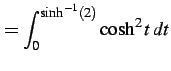 |
(1107) |
となる.
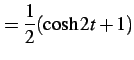 |
(1108) |
を用いると
![$\displaystyle =\frac{1}{2} \int_{0}^{\sinh^{-1}(2)}(\cosh 2t+1)\,dt= \left[\frac{1}{4}\sinh 2t+\frac{t}{2}\right]_{0}^{\sinh^{-1}(2)}$](img2121.png) |
(1109) | |
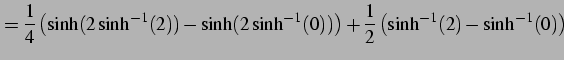 |
(1110) | |
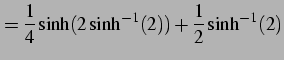 |
(1111) |
となる.ここで
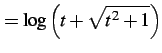 |
(1112) |
であることを用いると
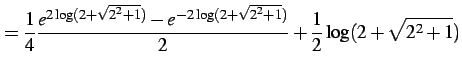 |
(1113) | |
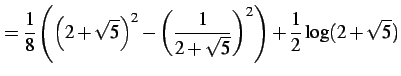 |
(1114) | |
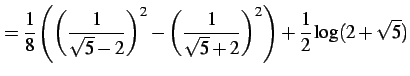 |
(1115) | |
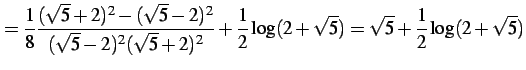 |
(1116) |
を得る.
Kondo Koichi

平成17年8月31日