Next: 16 線形写像の階数と退化次数 Up: 2 線形写像 Previous: 14 表現行列と基底の変換行列 Contents
15 線形写像の像と核
定義 2.65 (像,核)
線形写像 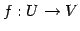 に対して次の集合を
に対して次の集合を
を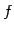 の像(image)という.
また,
の像(image)という.
また,
を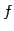 の核(kernel)という.
の核(kernel)という.
を
を
定理 2.66 (像,核と部分空間)
線形写像 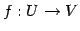 の像
の像
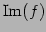 は
は
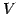 の部分空間である.
また,核
の部分空間である.
また,核
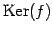 は
は 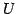 の部分空間である.
の部分空間である.
(証明)
Kondo Koichi

Created at 2004/12/13