Next: 6 線形写像の行列表示 Up: 2 線形写像 Previous: 4 全単射 Contents
5 線形写像
定義 2.19 (線形写像)
ベクトル空間 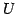 からベクトル空間
からベクトル空間 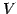 への写像
への写像
が
をみたすとき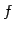 を線形写像(linear mapping)
または1 次写像という.
を線形写像(linear mapping)
または1 次写像という.
が
をみたすとき
![]() のとき
のとき ![]() を
線形変換(linear transformation)または
1 次変換という.
を
線形変換(linear transformation)または
1 次変換という.
注意 2.20 (零ベクトル)
線形写像 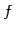 は零ベクトル
は零ベクトル
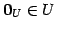 を
零ベクトル
を
零ベクトル
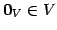 へ写す.
なぜなら,
へ写す.
なぜなら,
 とすると定義式より
とすると定義式より
となるからである.
となるからである.
例 2.21 (線形写像の具体例)
写像
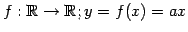 は線形写像である.
なぜなら,
は線形写像である.
なぜなら,
をみたすからである.
をみたすからである.
問 2.22 (線形写像)
次の写像は線形写像ではないことを示せ.
例 2.23 (線形写像の具体例)
写像
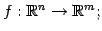
は線形写像である. なぜなら,
をみたすからである.
 |
は線形写像である. なぜなら,
をみたすからである.
問 2.24 (線形写像)
次の写像は線形写像ではないことを示せ.
例 2.25 (線形写像の具体例)
写像
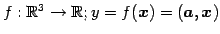 は
線形写像である.
ただし,
は
線形写像である.
ただし,
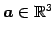 とする.
とする.
例 2.26 (線形写像の具体例)
写像
 は
線形変換である.
は
線形変換である.
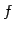 は点
は点
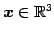 の平面
の平面
 への
射影変換である.
への
射影変換である.
Next: 6 線形写像の行列表示 Up: 2 線形写像 Previous: 4 全単射 Contents
Kondo Koichi

Created at 2004/12/13