Next: 5 線形写像 Up: 2 線形写像 Previous: 3 恒等写像,逆写像 Contents
4 全単射
定義 2.12 (定義域,値域)
写像 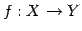 に関して,
に関して,
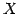 を定義域(domain)といい,
を定義域(domain)といい,
で定義される集合を 値域(range)または像(image)という.
で定義される集合を 値域(range)または像(image)という.
例 2.13 (値域の具体例)
写像
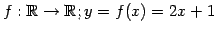 の
定義域は
の
定義域は
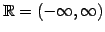 であり,
値域または
であり,
値域または 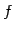 の像は
の像は
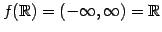 である.
である.
例 2.14 (値域の具体例)
写像
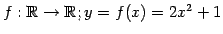 の
定義域は
の
定義域は
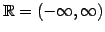 であり,
値域または
であり,
値域または 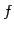 の像は
の像は
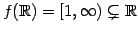 である.
である.
定義 2.15 (写像の分類)
写像 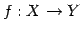 に対して次の分類を定義する.
に対して次の分類を定義する.
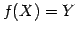 をみたすとき.
をみたすとき.
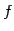 を上への写像(onto-mapping)
または全射(surjection)という.
を上への写像(onto-mapping)
または全射(surjection)という.
- 異なる 2 つの元
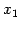 ,
,
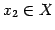 に対して
に対して
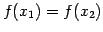 となるとき,
すなわち,
ある元
となるとき,
すなわち,
ある元 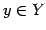 に対して
に対して 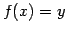 となる
ただ 1 つの元
となる
ただ 1 つの元 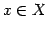 が定まるとき,
が定まるとき,
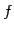 を1 対 1 写像(one-to-one mapping)
または単射(injection)という.
を1 対 1 写像(one-to-one mapping)
または単射(injection)という.
- 単射かつ全射のとき
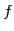 を
上への 1 対 1 写像(onto one-to-one mapping)または
全単射(bijection)という.
を
上への 1 対 1 写像(onto one-to-one mapping)または
全単射(bijection)という.
定理 2.16 (逆写像)
全単射のとき逆写像をもつ.
例 2.17 (全単射の具体例)
写像
は上への 1 対 1 写像である. また,このとき逆写像をもち,
と表される.
は上への 1 対 1 写像である. また,このとき逆写像をもち,
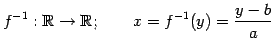 |
と表される.
例 2.18 (全単射ではない具体例)
写像
を考える.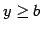 より
より
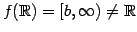 をみたし,
をみたし,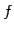 は上への写像ではない.
さらには,
は上への写像ではない.
さらには,
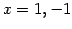 に対して
に対して 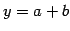 となり,
2 対 1 の写像であり 1 対 1 写像ではない.
またこれらより,逆写像
となり,
2 対 1 の写像であり 1 対 1 写像ではない.
またこれらより,逆写像 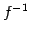 は存在しない.
は存在しない.
を考える.
Next: 5 線形写像 Up: 2 線形写像 Previous: 3 恒等写像,逆写像 Contents
Kondo Koichi

Created at 2004/12/13