Next: 18 基底 Up: 1 ベクトル空間 Previous: 16 部分空間 Contents
17 ベクトルで張られる空間
定義 1.76 (ベクトルによって生成される空間)
ベクトル
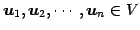 の
線形結合全体の集合を
の
線形結合全体の集合を
と定義する. この集合を ベクトル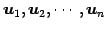 に
よって生成される(張られる)空間という.
に
よって生成される(張られる)空間という.
と定義する. この集合を ベクトル
定理 1.77 (ベクトルにより生成される空間と部分空間)
ベクトルにより生成される空間
は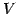 の部分空間である.
の部分空間である.
と表される. これらと任意のスカラー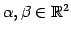 との
線形結合は
との
線形結合は
となる.よって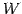 は部分空間である.
は部分空間である.
は
(証明)
![]() の任意の 2 つのベクトルは
の任意の 2 つのベクトルは
と表される. これらと任意のスカラー
となる.よって
例 1.78 (ベクトルによって生成される空間の具体例)
基本ベクトル
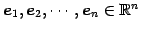 により生成される空間
により生成される空間
を考える.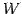 の任意のベクトルは
の任意のベクトルは
となる. 係数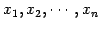 はすべての実数であるから,
ベクトル
はすべての実数であるから,
ベクトル 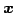 のなす集合は
のなす集合は
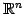 と等しい.
よって,
と等しい.
よって,
が成り立つ.
を考える.
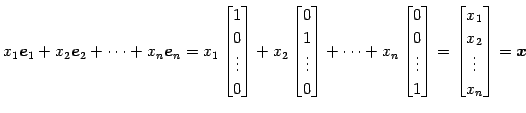 |
となる. 係数
が成り立つ.
例 1.79 (ベクトルによって生成される空間の具体例)
ベクトルにより生成される空間
を考える.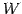 の任意のベクトルは
の任意のベクトルは
である. 2 つのスカラー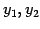 はすべての実数をとる.
ここで
はすべての実数をとる.
ここで
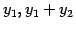 を新たな 2 つのスカラーと見なしてもよい.
すなわち,任意の実数
を新たな 2 つのスカラーと見なしてもよい.
すなわち,任意の実数 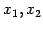 を用いて
を用いて
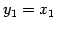 ,
,
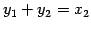 とおく.
このとき,
とおく.
このとき,
と表される. ベクトル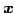 全体のなす集合は
全体のなす集合は
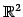 と等しい.
以上より,
と等しい.
以上より,
が成立する.
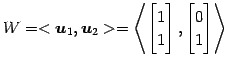 |
を考える.
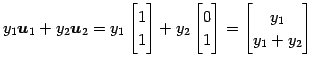 |
である. 2 つのスカラー
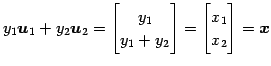 |
と表される. ベクトル
が成立する.
Next: 18 基底 Up: 1 ベクトル空間 Previous: 16 部分空間 Contents
Kondo Koichi

Created at 2004/12/13