Next: 18 行列式と面積 Up: 4 行列式 Previous: 16 行列の簡約化と行列式 Contents
17 ちょっとまとめ
定理 4.96 (行列式の性質)
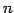 次正方行列
次正方行列 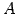 に対して次の条件は等価である.
に対して次の条件は等価である.
- (1)
-
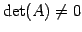
- (2)
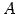 は正則である.
は正則である.
- (3)
-
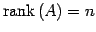
- (4)
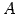 は
は 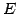 に簡約化される.
に簡約化される.
- (5)
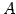 は逆行列
は逆行列
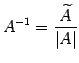 をもつ.
をもつ.
- (6)
- 方程式
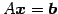 は一意な解
は一意な解
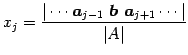 をもつ.
をもつ.
定理 4.97 (行列式の性質)
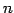 次正方行列
次正方行列 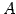 に対して次の条件は等価である.
に対して次の条件は等価である.
- (1)
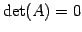
- (2)
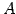 は非正則である.
は非正則である.
- (3)
-
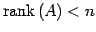
- (4)
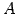 は
は 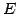 に簡約化されない.
に簡約化されない.
- (5)
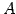 は逆行列をもたない.
は逆行列をもたない.
- (6)
- 方程式
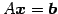 は一意な解をもたない.
は一意な解をもたない.
(任意定数を含む解をもつ.もしくは,解をもたない.)
Kondo Koichi

Created at 2004/11/26