Next: 17 ちょっとまとめ Up: 4 行列式 Previous: 15 クラメールの公式 Contents
16 行列の簡約化と行列式
注意 4.92 (基本変形行列の行列式)
行列の行の基本変形を表す行列
 ,
,
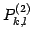 ,
,
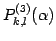 の行列式は
の行列式は
である.
| (761) |
である.
問 4.93 (基本変形行列の行列式)
これを示せ.
定理 4.94 (基本変形の正則性)
 が正則であるとき,行の基本変形をして得た行列
が正則であるとき,行の基本変形をして得た行列  もまた
正則である.
もまた
正則である.
となる.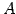 が正則なとき
が正則なとき
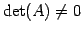 である.
である.
 であるから,
であるから,
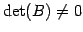 を得る.
よって
を得る.
よって 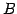 も正則である.
も正則である.
(証明)
行の基本変形は
![]() (
(![]() ) と表される.
両辺の行列式をとると
) と表される.
両辺の行列式をとると
| (762) |
となる.
定理 4.95 (行列の簡約化の正則性)
行列  が正則なとき
簡約化して得た階段行列
が正則なとき
簡約化して得た階段行列 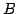 も正則である.
も正則である.
(証明)
簡約化は行の基本変形を繰り返し行う変換である.
正則な行列は正則な行列に写される.
これを繰り返して得られた行列 ![]() もまた正則である.
もまた正則である.
Kondo Koichi

Created at 2004/11/26