Next: 13 余因子行列 Up: 4 行列式 Previous: 11 余因子 Contents
12 余因子展開
定理 4.74 (余因子展開)
行列式 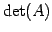 に対して
に対して
が成り立つ. これを第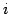 行に関する余因子展開という.
また,
行に関する余因子展開という.
また,
が成り立つ. これを第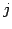 列に関する余因子展開という.
列に関する余因子展開という.
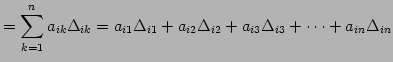 |
(700) | |
| (701) | ||
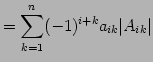 |
(702) |
が成り立つ. これを第
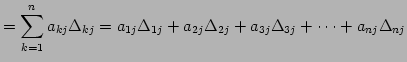 |
(703) | |
| (704) | ||
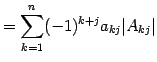 |
(705) |
が成り立つ. これを第
問 4.75 (余因子展開)
これを示せ.
となる. 次に第一行目の行ベクトルを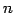 個のベクトルとしてみなし,
行列式を
個のベクトルとしてみなし,
行列式を 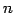 個に分解すると
個に分解すると
となる. 各項の第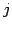 列を第一列に移動すると
列を第一列に移動すると
となる.各項を第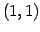 成分で展開すると
成分で展開すると
を得る. 同様の操作で列に関する余因子展開は示される.
(証明)
第 ![]() 行に関する余因子展開を示す.
まず行列式
行に関する余因子展開を示す.
まず行列式 ![]() の第
の第 ![]() 行目を第一行目に移動すると
行目を第一行目に移動すると
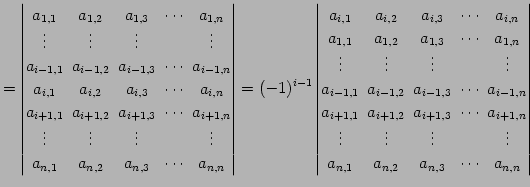 |
(706) |
となる. 次に第一行目の行ベクトルを
| (707) | ||
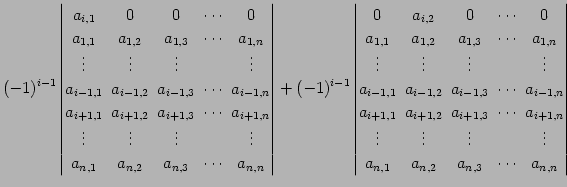 |
(708) | |
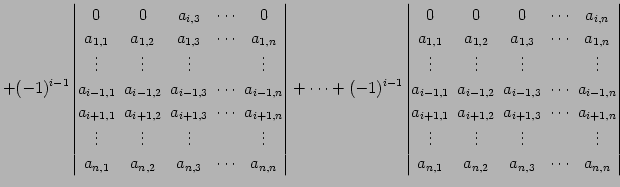 |
(709) |
となる. 各項の第
| (710) | ||
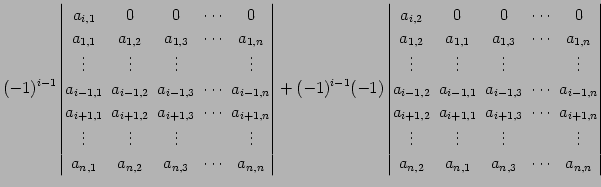 |
(711) | |
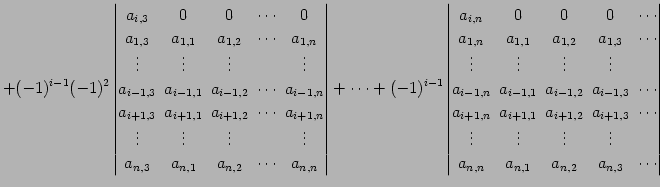 |
(712) |
となる.各項を第
| (713) | ||
| (714) | ||
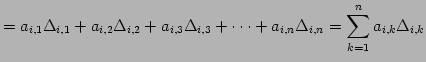 |
(715) |
を得る. 同様の操作で列に関する余因子展開は示される.
例 4.76 (余因子展開の計算例)
第 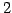 列目で余因子展開し,
列目で余因子展開し,
を得る.
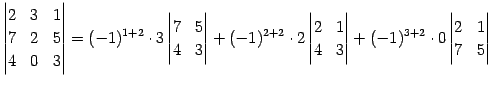 |
(716) | |
| (717) |
を得る.
例 4.77 (余因子展開の計算例)
第 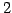 行目で余因子展開し,
行目で余因子展開し,
を得る.
 |
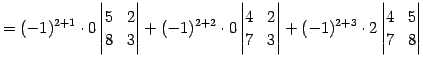 |
(718) |
| (719) |
を得る.
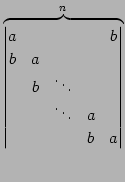
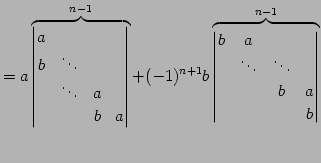
例 4.78 (余因子展開の計算例)
第一行目を余因子展開し,
を得る.
 |
 |
(720) |
| (721) |
を得る.
Next: 13 余因子行列 Up: 4 行列式 Previous: 11 余因子 Contents
Kondo Koichi

Created at 2004/11/26