7 行列式の計算

例 4.48 (行列式の計算の例)  

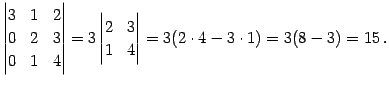$$\begin{vmatrix}3 & 1 & 2 \\ 0 & 2 & 3 \\ 0 & 1 & 4 \end{vmatrix}= 3 \begin{vmatrix}2 & 3 \\ 1 & 4 \end{vmatrix}= 3(2\cdot4-3\cdot1)= 3(8-3)=15\,.$$ (663)

例 4.49 (行列式の計算の例)   上三角行列の行列式：

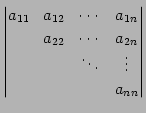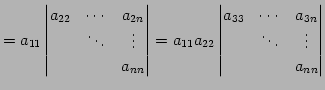$$\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ & a_{22} & \cdots & a_{2n} \\ & & \ddots & \vdots \\ & & & a_{nn} \end{vmatrix} = a_{11} \begin{vmatrix}a_{22} & \cdots & a_{2n} \\ & \ddots & \v... ...atrix}a_{33} & \cdots & a_{3n} \\ & \ddots & \vdots \\ & & a_{nn} \end{vmatrix}$$ (664)

$$=\cdots= a_{11}a_{22}a_{33}\cdots a_{nn}\,.$$ (665)

例 4.50 (行列式の計算の例)   下三角行列の行列式：

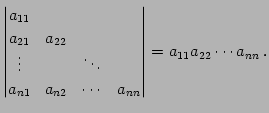$$\begin{vmatrix}a_{11} & & & \\ a_{21} & a_{22} & & \\ \vdots & & ... ...\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}= a_{11}a_{22}\cdots a_{nn}\,.$$ (666)

問 4.51 (下三角行列の行列式)   これを示せ．

例 4.52 (行列式の計算の例)   対角行列の行列式：

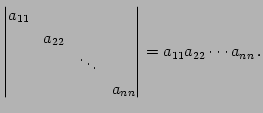$$\begin{vmatrix}a_{11} & & & \\ & a_{22} & & \\ & & \ddots & \\ & & & a_{nn} \end{vmatrix}= a_{11}a_{22}\cdots a_{nn}\,.$$ (667)

問 4.53 (対角行列の行列式)   これを示せ．

例 4.54 (行列式の計算の例)   単位行列の行列式：

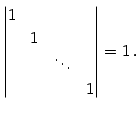$$\begin{vmatrix}1 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{vmatrix}=1\,.$$ (668)

例 4.55 (行列式の計算の例)  

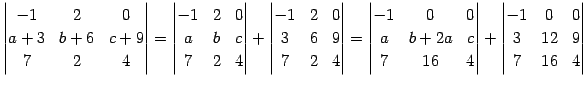$$\begin{vmatrix}-1 & 2 & 0 \\ a+3 & b+6 & c+9 \\ 7 & 2 & 4 \end{vm... ...{vmatrix} + \begin{vmatrix}-1 & 0 & 0 \\ 3 & 12 & 9 \\ 7 & 16 & 4 \end{vmatrix}$$ (669)

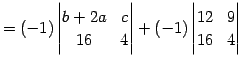$$= (-1) \begin{vmatrix}b+2a & c \\ 16 & 4 \end{vmatrix} + (-1) \begin{vmatrix}12 & 9 \\ 16 & 4 \end{vmatrix}$$ (670)

$$= -(4(b+2a)-16c)-(12\cdot4-9\cdot16)= -8a-4b+16c+96\,.$$ (671)

例 4.56 (行列式の計算の例)  

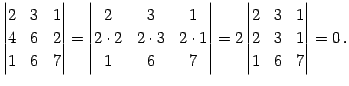$$\begin{vmatrix}2 & 3 & 1 \\ 4 & 6 & 2 \\ 1 & 6 & 7 \end{vmatrix}=... ...atrix}= 2 \begin{vmatrix}2 & 3 & 1 \\ 2 & 3 & 1 \\ 1 & 6 & 7 \end{vmatrix}=0\,.$$ (672)

例 4.57 (行列式の計算の例)  

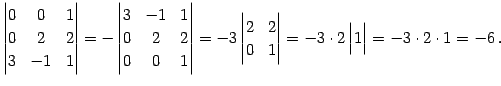$$\begin{vmatrix}0 & 0 & 1 \\ 0 & 2 & 2 \\ 3 & -1 & 1 \end{vmatrix}... ...1 \end{vmatrix}= -3\cdot2 \begin{vmatrix}1 \end{vmatrix}= -3\cdot2\cdot1= -6\,.$$ (673)

例 4.58 (行列式の計算の例)  

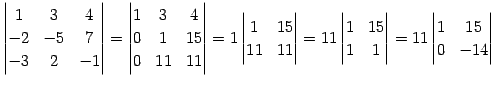$$\begin{vmatrix}1 & 3 & 4 \\ -2 & -5 & 7 \\ -3 & 2 & -1 \end{vmatr... ... & 15 \\ 1 & 1 \end{vmatrix}= 11 \begin{vmatrix}1 & 15 \\ 0 & -14 \end{vmatrix}$$ (674)

$$= 11\cdot1 \begin{vmatrix}-14 \end{vmatrix}= 11\cdot(-14)= -154\,.$$ (675)

例 4.59 (行列式の計算の例)  

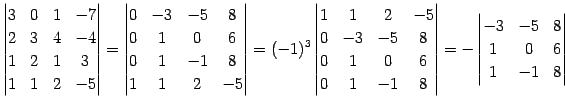$$\begin{vmatrix}3 & 0 & 1 & -7 \\ 2 & 3 & 4 & -4 \\ 1 & 2 & 1 & 3 ... ...vmatrix}= - \begin{vmatrix}-3 & -5 & 8 \\ 1 & 0 & 6 \\ 1 & -1 & 8 \end{vmatrix}$$ (676)

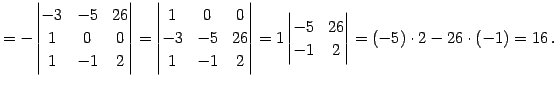$$= - \begin{vmatrix}-3 & -5 & 26 \\ 1 & 0 & 0 \\ 1 & -1 & 2 \end{v... ... 1 \begin{vmatrix}-5 & 26 \\ -1 & 2 \end{vmatrix}= (-5)\cdot2-26\cdot(-1)=16\,.$$ (677)

例 4.60 (行列式の計算の例)  

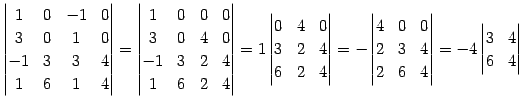$$\begin{vmatrix}1 & 0 & -1 & 0 \\ 3 & 0 & 1 & 0 \\ -1 & 3 & 3 & 4 ... ... & 4 \\ 2 & 6 & 4 \end{vmatrix}= -4 \begin{vmatrix}3 & 4 \\ 6 & 4 \end{vmatrix}$$ (678)

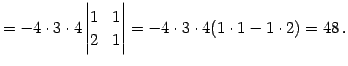$$= -4\cdot3\cdot4 \begin{vmatrix}1 & 1 \\ 2 & 1 \end{vmatrix}= -4\cdot3\cdot4(1\cdot1-1\cdot2)= 48\,.$$ (679)

Kondo Koichi
Created at 2004/11/26