Next: 10 行列のベクトルへの分割 Up: 2 行列とベクトル Previous: 8 行列の分割 Contents
9 分割された行列の積
定理 2.65 (分割された行列の積)
行列
![$ A=[a_{ij}]_{m\times n}$](img1173.png) ,
,
![$ B=[b_{ij}]_{n\times r}$](img1174.png) を分割し,
を分割し,
と表したとき,行列の積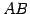 は
は
と与えられる.
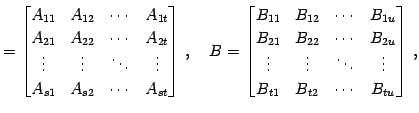 |
(290) | |
| (291) | ||
| (292) | ||
| (293) | ||
| (294) | ||
| (295) |
と表したとき,行列の積
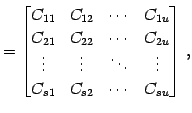 |
(296) | |
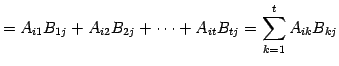 |
(297) |
と与えられる.
問 2.66
これを示せ.
例 2.67 (分割された行列の積の具体例)
行列
の積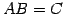 を考える.
このとき行列を分割し
を考える.
このとき行列を分割し
とする.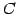 の部分行列は
の部分行列は
となるので,結局積として
を得る.
![$\displaystyle = \left[ \begin{array}{cc\vert c\vert cc} 1 & 2 & 4 & 5 & 1 \\ \h...
... -1 & 2 \\ 0 & 3 \\ \hline 1 & -2 \\ \hline -1 & 1 \\ 2 & -3 \end{array}\right]$](img1188.png) |
(298) |
の積
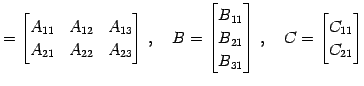 |
(299) |
とする.
| (300) | ||
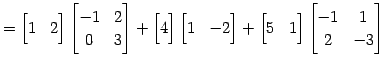 |
(301) | |
| (302) | ||
| (303) | ||
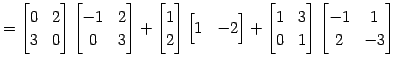 |
(304) | |
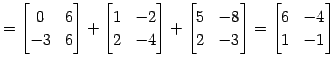 |
(305) |
となるので,結局積として
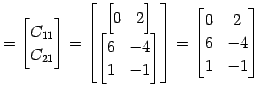 |
(306) |
を得る.
例 2.68 (分割された行列の積の計算例)
(証明)
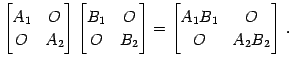 |
(307) |
(証明)
(左辺)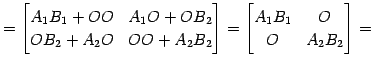 (右辺) (右辺) |
(308) |
例 2.69 (分割された行列の積の計算例)
行列の積
を考える. これは
という形をしている. よって積は
と求まる.
![$\displaystyle \left[\begin{array}{cc\vert cc} 2 & 1 & 1 & 0 \\ 4 & 3 & 0 & 1 \\...
...\\ 3 & 2 & 0 & 1 \\ \hline 0 & 0 & 2 & 1 \\ 0 & 0 & 1 & 0 \\ \end{array}\right]$](img1206.png) |
(309) |
を考える. これは
![$\displaystyle \left[\begin{array}{c\vert c} A & E \\ \hline O & B \end{array}\right] \left[\begin{array}{c\vert c} C & E \\ \hline O & D \end{array}\right]$](img1207.png) |
(310) |
という形をしている. よって積は
![$\displaystyle \left[ \begin{array}{c\vert c} AC & A+D \\ \hline O & BD \end{arr...
...1 \end{bmatrix} \begin{bmatrix}2 & 1 \\ 1 & 0 \end{bmatrix} \end{array} \right]$](img1208.png) |
(311) | |
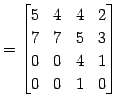 |
(312) |
と求まる.
Next: 10 行列のベクトルへの分割 Up: 2 行列とベクトル Previous: 8 行列の分割 Contents
Kondo Koichi

Created at 2004/11/26