Next: 6 ЙдЮѓЄЮБщЛЛЄЫДиЄЙЄыНяРМС Up: 5 ЙдЮѓЄЮБщЛЛ Previous: 2 ЙдЮѓЄЮЅЙЅЋЅщЁМЧм Contents
3 ЙдЮѓЄЮРб
ФъЕС 2.46 (ЙдЮѓЄЮРб)
ЙдЮѓ 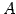 ЄШЙдЮѓ
ЄШЙдЮѓ 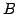 ЄЮРбЄђ
ЄЮРбЄђ 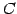 ЄШЄЙЄыЁЅ
ЄГЄЮЄШЄ
ЄШЄЙЄыЁЅ
ЄГЄЮЄШЄ
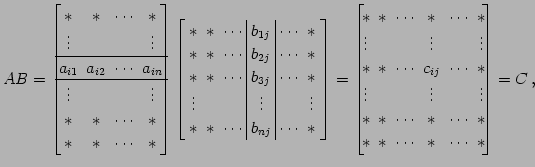
ЄШЩНЕЄЙЄыЁЅ ЙдЮѓЄЮРбЄЯЗПЄЌ
ЄЮЄШЄФъЕСЄЕЄьЄыЁЅ ГЦРЎЪЌЄЯ
ЄШФъЕСЄЕЄьЄыЁЅ
| (244) |
ЄШЩНЕЄЙЄыЁЅ ЙдЮѓЄЮРбЄЯЗПЄЌ
| (245) |
ЄЮЄШЄФъЕСЄЕЄьЄыЁЅ ГЦРЎЪЌЄЯ
 |
(246) | |
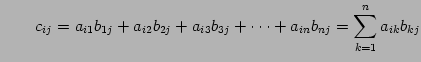 |
(247) |
ЄШФъЕСЄЕЄьЄыЁЅ
Юу 2.47 (ЙдЮѓЄЮРбЄЮЗзЛЛЮу)
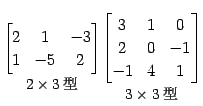 |
(248) | |
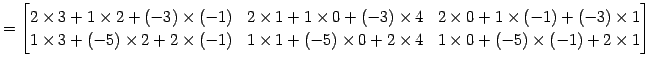 |
(249) | |
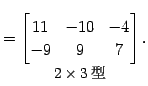 |
(250) |
Юу 2.48 (ЙдЮѓЄЮРбЄЮЗзЛЛЮу)
ЄШЄЊЄЏЁЅ
 ЄЧЄЂЄыЄГЄШЄЫУэАеЁЅ
ЄЧЄЂЄыЄГЄШЄЫУэАеЁЅ
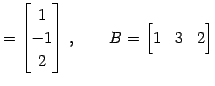 |
(251) |
ЄШЄЊЄЏЁЅ
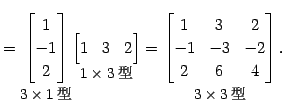 |
(252) | |
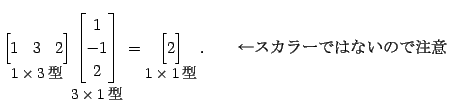 |
(253) |
Юу 2.49 (ЙдЮѓЄЮРбЄЮЖёТЮЮу)
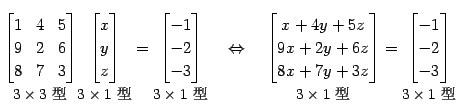 |
(254) | |
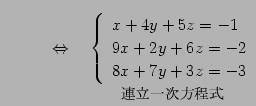 |
(255) |
Next: 6 ЙдЮѓЄЮБщЛЛЄЫДиЄЙЄыНяРМС Up: 5 ЙдЮѓЄЮБщЛЛ Previous: 2 ЙдЮѓЄЮЅЙЅЋЅщЁМЧм Contents
Kondo Koichi

Created at 2004/11/26