Next: 3 行列の積 Up: 5 行列の演算 Previous: 1 行列の和と差 Contents
2 行列のスカラー倍
定義 2.43 (行列のスカラー倍)
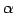 をスカラー(数)とする.
行列
をスカラー(数)とする.
行列 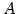 のスカラー倍を
のスカラー倍を
と表記する. 行列のスカラー倍は型が
のとき定義される. 各成分は
と定義される.
| (239) |
と表記する. 行列のスカラー倍は型が
| (240) |
のとき定義される. 各成分は
| (241) |
と定義される.
例 2.44 (スカラー倍の計算例)
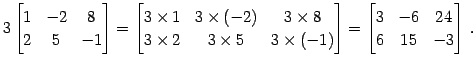 |
(242) |
例 2.45 (スカラー倍の計算例)
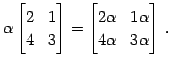 |
(243) |
Kondo Koichi

Created at 2004/11/26