17 外積の性質

定理 1.72 (外積の性質)    

(i)

$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$.

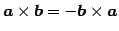(ii)

$\vec{a}\times\vec{a}=0$.

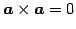(iii)

$\vec{a}\parallel\vec{b}\Leftrightarrow\vec{a}\times\vec{b}=0$.

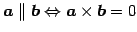問 1.73 (外積の性質)   これを示せ．

（証明） (i) 積の順を入れ換えると向きが反対向きになるため． (ii) 自分自身との角度は $\theta=0$ であるから長さは 0 となり， 外積は $\vec{0}$ である． (iii) $\vec{a}$ と $\vec{b}$ が並行なとき $\theta=0$ であるから長さは 0 となり， 外積は $\vec{0}$ である．

注意 1.74 (内積の性質)   外積の性質と内積の性質の違いに注意する：

(i)

$\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$.

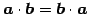(ii)

$\vec{a}\cdot\vec{a}=\Vert\vec{a}\Vert^2$.

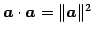(iii)

$\vec{a}\perp\vec{b}\Leftrightarrow\vec{a}\cdot\vec{b}=0$.

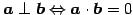定理 1.75 (外積の性質)    

(i)

$\vec{a}\times(\vec{b}+\vec{c})= \vec{a}\times\vec{b}+\vec{a}\times\vec{c}$,     $(\vec{a}+\vec{b})\times\vec{c}= \vec{a}\times\vec{c}+\vec{b}\times\vec{c}$.

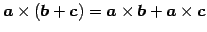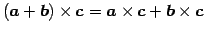(ii)

$(\alpha\vec{a})\times\vec{b}=\alpha(\vec{a}\times\vec{b})= \vec{a}\times(\alpha\vec{b})$.

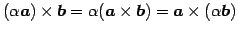問 1.76 (外積の性質)   これを示せ．

定理 1.77 (外積の性質)    

(i)

$(\vec{a}\times\vec{b})\cdot\vec{a}=0$,     $(\vec{a}\times\vec{b})\cdot\vec{b}=0$.

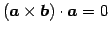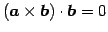(ii)

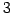ベクトル $3$ 重積（vector triple product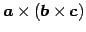） $\vec{a}\times(\vec{b}\times\vec{c})$ に関して
$(\vec{a}\times\vec{b})\times\vec{c}= (\vec{a}\cdot\vec{c})\vec{b}-(\vec{b}\cdot\vec{c})\vec{a}$,
$\vec{a}\times(\vec{b}\times\vec{c})= (\vec{a}\cdot\vec{c})\vec{b}-(\vec{a}\cdot\vec{b})\vec{c}$
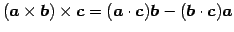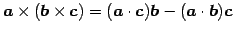
が成り立つ． これをラグランジュの公式（Lagrange's formula）と呼ぶ．

(iii)

$(\vec{a}\times\vec{b})\times\vec{c}+ (\vec{b}\times\vec{c})\times\vec{a}+ (\vec{c}\times\vec{a})\times\vec{b}=0$.
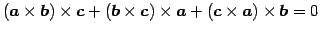これをヤコビの公式（Jacobi's formula）と呼ぶ．

(iv)

$(\vec{a}\times\vec{b})\cdot(\vec{c}\times\vec{d})= (\vec{a}\cdot\vec{c})(\vec{b}\cdot\vec{d})- (\vec{a}\cdot\vec{d})(\vec{b}\cdot\vec{c})$.

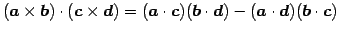問 1.78 (外積の性質)   これを示せ．

Kondo Koichi
Created at 2004/11/26