Next: 3 連続性 Up: 1 偏微分 Previous: 1 変数関数 Contents
2 極限
定義 1.8 (極限)
定義域内の点 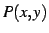 を点
を点 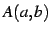 に近づける.
ただし
に近づける.
ただし
 とする.
このとき,
近づけ方に依らず関数
とする.
このとき,
近づけ方に依らず関数 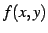 の値が
同じ一つの値
の値が
同じ一つの値 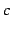 に近づくならば,
に近づくならば,
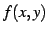 は極限
は極限 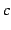 が存在するという.
が存在するという.
| (8) |
Kondo Koichi

Created at 2004/10/21



Next: 3 連続性 Up: 1 偏微分 Previous: 1 変数関数 Contents
2 極限
定義 1.8 (極限) 定義域内の点を点
に近づける. ただし
とする. このとき, 近づけ方に依らず関数
の値が 同じ一つの値
に近づくならば,
は極限
が存在するという.
(8)
Kondo Koichi


Created at 2004/10/21