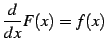Next: 2 不定積分の性質 Up: 6 積分法 Previous: 6 積分法 Contents
1 不定積分
関数 ![]() に関して
に関して ![]() で``微分をする''という操作を
で``微分をする''という操作を
![]() という
演算子,作用素(operator)で表すとする.
すなわち関数
という
演算子,作用素(operator)で表すとする.
すなわち関数 ![]() に微分演算
に微分演算
![]() を作用させるとは
を作用させるとは
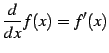 |
(783) |
のことである. この微分演算の逆演算を考える. これを
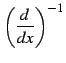 と表記し
と表記し
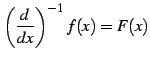 |
(784) |
と表すことにする. 逆演算により得られる関数
を満たす関数と定義する. 定義からただちに分かるように, ある関数
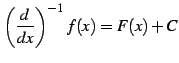 |
(786) |
が成り立つ. 微分の逆演算
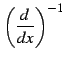 は
通常
は
通常
| (787) |
と表せる.
定義 6.1 (不定積分)
関数 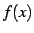 に対して,
微分演算
に対して,
微分演算
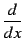 の
逆演算を
の
逆演算を
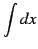 と表記し,
と表記し,
と定義する.ただし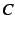 は任意定数である.
は任意定数である.
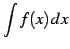 を不定積分(indefinite integral),
を不定積分(indefinite integral),
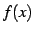 を被積分関数(integrand),
を被積分関数(integrand),
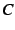 を積分定数(constant of integration),
を積分定数(constant of integration),
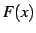 を原始関数(primitive function)と呼ぶ.
を原始関数(primitive function)と呼ぶ.
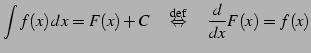 |
(788) |
と定義する.ただし
Kondo Koichi

Created at 2004/08/14