Next: 13 級の関数 Up: 3 微分法 Previous: 11 逆双曲線関数の微分 Contents
12 高階導関数
定義 3.32 (高階導関数)
関数 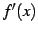 が微分可能のとき,
が微分可能のとき, の導関数
の導関数
を2 階導関数(second order derivative)という. このとき は
2 回微分可能(two times differentiable)と呼ぶ.
同様に
は
2 回微分可能(two times differentiable)と呼ぶ.
同様に 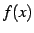 を
を  回繰り返し微分した関数を
回繰り返し微分した関数を
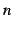 階導関数(
階導関数( -th order derivative)といい,
-th order derivative)といい,
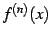 と書き表わす.
関数
と書き表わす.
関数
 は
は
と再帰的に定義する. ただし とする.
とする.
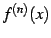 が存在するとき
が存在するとき  は
は
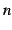 回微分可能(
回微分可能( times differentiable)という.
times differentiable)という.
 |
(313) |
を2 階導関数(second order derivative)という. このとき
 |
(314) |
と再帰的に定義する. ただし
例 3.33 (高階導関数の計算例)
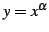 の高階導関数を求める.
の高階導関数を求める.
 が自然数ではないとき,
が自然数ではないとき,
を得る. が自然数
が自然数 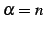 のとき,
のとき,
を得る.
| (315) | ||
| (316) | ||
| (317) | ||
| (318) | ||
| (319) | ||
を得る.
| (320) | ||
| (321) | ||
| (322) | ||
| (323) | ||
| (324) | ||
| (325) | ||
| (326) | ||
| (327) | ||
を得る.
例 3.34 (高階導関数の計算例)
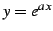 の高階導関数を求める.
合成関数の微分を繰り返して
の高階導関数を求める.
合成関数の微分を繰り返して
を得る.
| (328) | ||
| (329) | ||
| (330) | ||
| (331) | ||
| (332) |
を得る.
例 3.35 (高階導関数の計算例)
| (333) | ||
| (334) | ||
| (335) | ||
| (336) | ||
| (337) | ||
| (338) | ||
 |
(339) | |
| (340) |
問 3.36 (高階導関数の例)
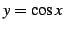 ,
, 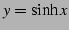 ,
,  の
の  を求めよ.
を求めよ.
例 3.37 (高階導関数の計算例)
ただし
と定義する.
| (341) | ||
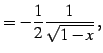 |
(342) | |
 |
(343) | |
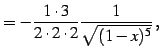 |
(344) | |
 |
(345) | |
| (346) | ||
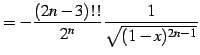 |
(347) |
ただし
| (348) | ||
| (349) | ||
| (350) |
と定義する.
問 3.38
参考書(p.52)問題 3-3.
Next: 13 級の関数 Up: 3 微分法 Previous: 11 逆双曲線関数の微分 Contents
Kondo Koichi

Created at 2004/08/14