Next: 15 逆双曲線関数 Up: 2 関数 Previous: 13 逆三角関数 Contents
14 双曲線関数
双曲線関数(hyperbolic function)とは
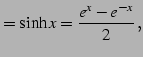 |
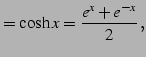 |
 |
(70) |
により定義される関数である. 関数の読み方は上から hyperbolic sine, hyperbolic cosine, hyperbolic tangent である. また双曲線関数の逆数を
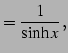 |
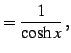 |
 |
(71) |
と定義する.
注意 2.40 (三角関数と双曲線関数)
三角関数は複素関数を用いて次のようにも定義される:
双曲線関数の定義との類似に注意せよ.
 |
(72) | |
 |
(73) | |
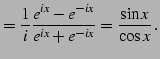 |
(74) |
双曲線関数の定義との類似に注意せよ.
問 2.41 (双曲線関数の概形)
双曲線関数の概形を書け.
定理 2.42 (双曲線関数の性質)
双曲線関数は次の性質をもつ.
| (75) | ||
| (76) | ||
| (77) | ||
| (78) | ||
| (79) | ||
| (80) | ||
 |
(81) |
問 2.43 (双曲線関数の性質)
この性質を証明せよ.
(証明)双曲線関数の定義をそのまま用いれば証明できる.
問 2.44 (双曲線関数の性質)
次の式を導け.
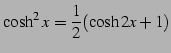 |
(82) | |
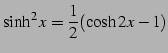 |
(83) | |
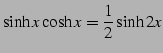 |
(84) | |
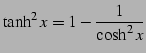 |
(85) |
問 2.45 (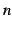 倍角の公式)
倍角の公式)
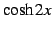 ,
,  ,
, 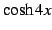 ,
,  を
を
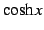 の多項式で表せ.
の多項式で表せ.
(答え)
| (86) | ||
| (87) | ||
| (88) |
問 2.46 (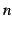 倍角の公式)
倍角の公式)
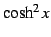 ,
, 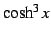 ,
, 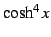 ,
,  を
を
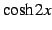 ,
,  ,
, 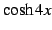 ,
, 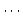 の線形結合で表せ.
の線形結合で表せ.
より
となるので
を得る.
(答え)
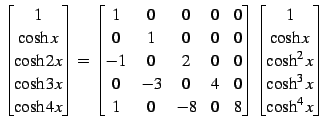 |
(89) |
より
 |
(90) |
となるので
 |
(91) | |
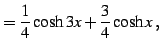 |
(92) | |
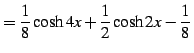 |
(93) |
を得る.
問 2.47 (円と双曲線)
円 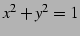 をパラメータ表示すると
をパラメータ表示すると
と表わせる. 双曲線 をパラメータ表示するには
をパラメータ表示するには
とおけばよい. これを示せ.
| (94) |
と表わせる. 双曲線
| (95) |
とおけばよい. これを示せ.
注意 2.48 (円関数)
双曲線関数に対して三角関数は円関数と呼ぶこともある.
Next: 15 逆双曲線関数 Up: 2 関数 Previous: 13 逆三角関数 Contents
Kondo Koichi

Created at 2004/08/14