Next: 3 関数のグラフ Up: 2 関数 Previous: 1 写像 Contents
2 関数
関数(function)とは,
ある値 ![]() が与えられたとき,
何らかの演算規則
が与えられたとき,
何らかの演算規則 ![]() に従って値
に従って値 ![]() を定め,
その値
を定め,
その値 ![]() を返す機能のことである.
関数は
を返す機能のことである.
関数は
| (19) |
と書き表される. 例えばある関数を
| (20) | ||||||
| (21) | ||||||
| (22) | ||||||
| (23) |
のように,
入力 ![]() にある変換
にある変換 ![]() を作用させ出力
を作用させ出力 ![]() を返す.これを
を返す.これを
| (24) |
と表す.
定義 2.1 (関数に関する名称)
関数 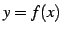 に関連して次の名称を定義する:
に関連して次の名称を定義する:
- 定数(constant)
 一定の値を表す数.
一定の値を表す数.
- 変数(variable)
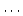 変化する値を表す数.
変化する値を表す数.
- 独立変数(independent variable)
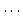 自由に値を定めることができる変数
自由に値を定めることができる変数 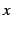 のこと.
のこと.
- 従属変数(dependent variable)
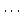 独立変数
独立変数 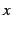 に応じて値が変化する変数
に応じて値が変化する変数 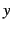 のこと.
のこと.
- 定義域,変域(domain)
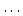 独立変数
独立変数 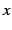 がとり得る範囲
がとり得る範囲 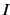 .
.
- 値域(range)
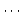 従属変数
従属変数  がとり得る範囲
がとり得る範囲 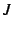 .
.
例 2.2 (関数に関する名称の具体例)
関数
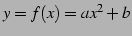 を考える.
このとき
を考える.
このとき 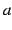 ,
, 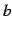 は定数であり,
は定数であり,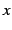 ,
, 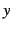 は変数である.
また
は変数である.
また 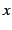 は独立変数であり,
は独立変数であり, は従属変数である.
定義域は
は従属変数である.
定義域は
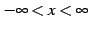 であり,
値域は
であり,
値域は
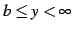 である.
である.
Next: 3 関数のグラフ Up: 2 関数 Previous: 1 写像 Contents
Kondo Koichi

Created at 2004/08/14