Next: 6 対数関数の微分 Up: 3 微分法 Previous: 4 定数の微分 Contents
5 巾関数の微分
定理 3.13 (巾関数の微分)
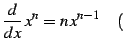 |
(362) |
問 3.14
これを示せ.
を得る.ここで
であることを用いると
となる.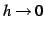 のとき
のとき
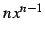 の項は生き残り,
その後ろの項は消える.
よって
の項は生き残り,
その後ろの項は消える.
よって
を得る.
(証明)
![]() とおき定義に従い計算すると,
とおき定義に従い計算すると,
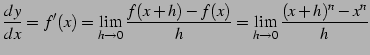 |
(363) |
を得る.ここで
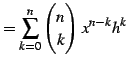 |
(364) | |
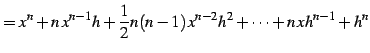 |
(365) | |
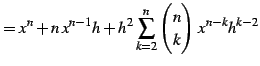 |
(366) |
であることを用いると
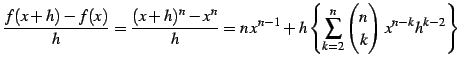 |
(367) |
となる.
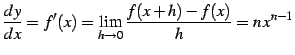 |
(368) |
を得る.
定理 3.15 (負巾関数の微分)
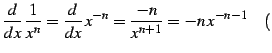 |
(369) |
問 3.16
これを示せ.
となる.これを用いて
を得る.
(証明)
![]() とおく.
このとき
とおく.
このとき
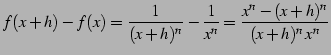 |
(370) | |
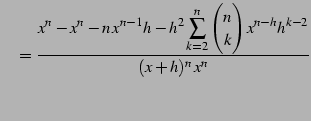 |
(371) | |
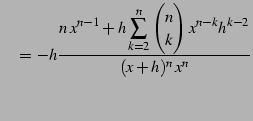 |
(372) |
となる.これを用いて
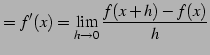 |
(373) | |
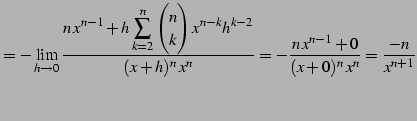 |
(374) |
を得る.
定理 3.17 (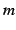 乗根関数の微分)
乗根関数の微分)
![$\displaystyle \frac{d}{dx}\,\sqrt[m]{x}= \frac{d}{dx}\,x^{\frac{1}{m}}= \frac{\sqrt[m]{x}}{m\,x}= \frac{1}{m}\,x^{\frac{1}{m}-1} \quad($](img1271.png) |
(375) |
問 3.18
これを示せ.
である. ここで
であることを用いる.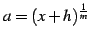 ,
,
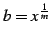 とおくと
とおくと
を得る.よって
となる.
(証明)
![]() とおく.
このとき
とおく.
このとき
| (376) |
である. ここで
| (377) | ||
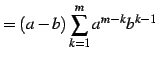 |
(378) | |
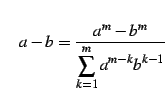 |
(379) |
であることを用いる.
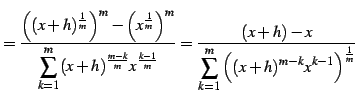 |
(380) | |
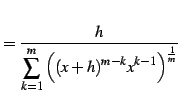 |
(381) |
を得る.よって
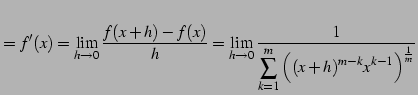 |
(382) | |
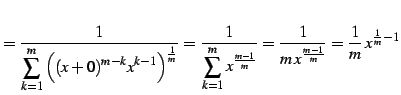 |
(383) |
となる.
定理 3.19 (巾関数の微分)
と表されるのでこれを微分すると
を得る.
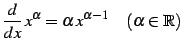 |
(384) |
(証明)
次節の
![]() ,
,
![]() が既に証明済みであるとする.
このとき
が既に証明済みであるとする.
このとき
| (385) |
と表されるのでこれを微分すると
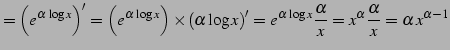 |
(386) |
を得る.
Next: 6 対数関数の微分 Up: 3 微分法 Previous: 4 定数の微分 Contents
Kondo Koichi
Created at 2003/08/29