9 対数関数

指数関数の逆関数を対数関数（logarithmic function）といい，

$$y =\log_{a}x\,\qquad(x>0)$$ (174)

と表される．$y$ は $a$ を底（base）とする $x$ の対数（logarithm）であると読む． 特に $a=10$ のとき常用対数（common logarithm） と呼び $y=\log x$ と書く． また $a=e$ のとき自然対数（natural logarithm）と呼び $y=\log x$ または $y=\ln x$ と書く．

定理 2.18 (対数関数の性質)   対数関数は次の性質をもつ：

(1)

$\log_{a}xy=\log_{a}x+\log_{a}y$.

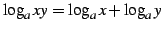(2)

$${ \log_{a}\left(\frac{x}{y}\right)=\log_{a}x-\log_{a}y}$$.

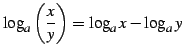(3)

$\log_{a}x^y=y\log_{a}x$.

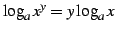(4)

$${\log_{b}x=\frac{\log_{a}x}{\log_{a}b}}$$.

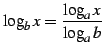問 2.19 (対数関数の性質)   この性質を示せ．

（答え） 対数関数は指数関数の逆関数であることと 指数関数の性質を用いて示す．

問 2.20 (対数関数のグラフ)   対数関数のグラフを書け．

Kondo Koichi
Created at 2003/08/29