Next: 9 収束する数列のいろいろ Up: 1 数列と極限 Previous: 7 数列の極限 Contents
8 数列の極限に関する定理
定理 1.20 (数列の極限に関する定理)
| (27) |
定理 1.21 (数列の極限に関する定理)
数列 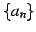 ,
, 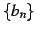 に関して極限
に関して極限
が存在するとき,次の関係式が成り立つ:
ただし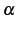 ,
, 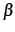 は定数とする.
は定数とする.
| (28) |
が存在するとき,次の関係式が成り立つ:
| (29) | ||
| (30) | ||
| (31) | ||
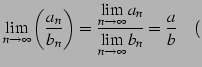 |
(32) |
ただし
注意 1.22 (不定形)
上の定理は四則演算と極限の操作を交換可能であることを意味している.
しかし,定理が適用可能なのは,
現れる数列それぞれが有限確定するときのみである.
もし極限の計算結果が不定形
となるときは, 途中の計算過程で定理が適用不可能となっている. 計算結果が次のようなときは有限または無限確定である:
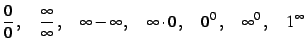 |
(33) |
となるときは, 途中の計算過程で定理が適用不可能となっている. 計算結果が次のようなときは有限または無限確定である:
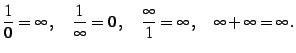 |
(34) |
定理 1.23 (はさみうちの定理)
数列 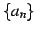 ,
, 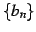 ,
, 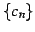 が
が
を満たすとき,
ならば,
が成り立つ.
| (35) |
を満たすとき,
| (36) |
ならば,
| (37) |
が成り立つ.
Next: 9 収束する数列のいろいろ Up: 1 数列と極限 Previous: 7 数列の極限 Contents
Kondo Koichi
Created at 2003/08/29