Zabusky & Kruskal の KdV 方程式の数値シュミレーション
KdV equation:
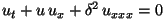 ,
,
where
u = u ( x, t )
and
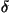 =0.022.
=0.022.
1 soliton solution:
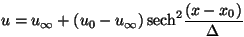 ,
,
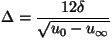 .
.
Boundary condition:
u ( x + L, t ) =
u ( x, t ).
Numerical scheme of KdV equation:
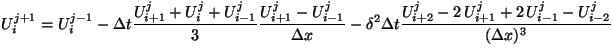 ,
,
where
i = 0, 1, ..., N-1,
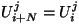 and
and
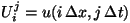 .
.
Parameters:
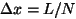 ,
,
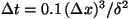 ,
N=128
and
L=2.
,
N=128
and
L=2.
The source.
- [1]
N. J. Zabusky and M. D. Kruskal: Integration of "solitons" in a
collisionless plasma and recurrence of initial states,
Phys. Rev. Lett. 15 (1965), 240--243.
(C)
Kondo Koichi, 2007/08/21
[email protected]
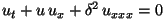 ,
,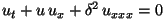 ,
,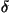 =0.022.
=0.022.
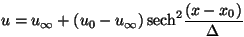 ,
,
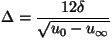 .
.
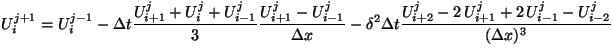 ,
,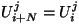 and
and
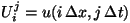 .
.
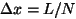 ,
,
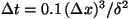 ,
N=128
and
L=2.
,
N=128
and
L=2.